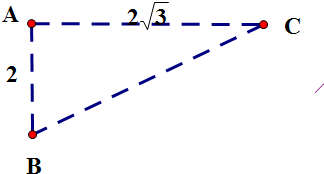
已知A，B，C是球O的球面上三点，AB=2，AC=23，∠ABC=60°，且棱锥O-ABC的体积为463，则球O的表面积为（）A.10πB.24πC.36πD.48π

Question

已知A，B，C是球O的球面上三点，AB=2，AC=2

√(3)，∠ABC=60°，且棱锥O-ABC的体积为(4√(6))/(3)，则球O的表面积为（　　）

A. 10π

B. 24π

C. 36π

D. 48π

Answer 1

∵AB=2，AC=2√(3)，∠ABC=60°
∴(c)/(sinC)=(a)/(sinA)=(b)/(sinB)，
(2)/(sinC)=(2√(3))/(sin60°)，C<60°，
sinC=(1)/(2)，C=30°，
∴∠A=90°，BC=√(22+12)=4
∵A，B，C是球O的球面上三点
∴截面圆的圆心为AC中点，
半径为2
∵棱锥O-ABC的体积为(4√(6))/(3)，
∴(1)/(3)×(1)/(2)×2×2√(3)×d=(4√(6))/(3)，∴d=2√(2)，
∴R²=（2√(2)）²+2²=12，



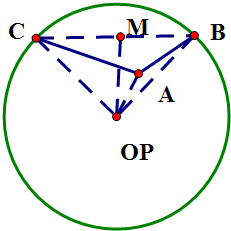
∴球O的表面积为：4πR²=48π，
故选：D．