早教吧作业答案频道 -->数学-->
如图,矩形ABCD中,AB=9,AD=4.E为CD边上一点,CE=6.点P从点B出发,以每秒1个单位的速度沿着边BA向终点A运动,连接PE.设点P运动的时间为t秒.(1)求AE的长;(2)当t为何值时,△PAE为直
题目详情
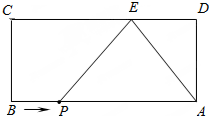
如图,矩形ABCD中,AB=9,AD=4.E为CD边上一点,CE=6.点P从点B出发,以每秒1个单位的速度沿着边BA向终点A运动,连接PE.设点P运动的时间为t秒.
(1)求AE的长;
(2)当t为何值时,△PAE为直角三角形?
(3)是否存在这样的t,使EA恰好平分∠PED,若存在,求出t的值;若不存在,请说明理由.

(1)求AE的长;
(2)当t为何值时,△PAE为直角三角形?
(3)是否存在这样的t,使EA恰好平分∠PED,若存在,求出t的值;若不存在,请说明理由.
▼优质解答
答案和解析
(1)∵矩形ABCD中,AB=9,AD=4,
∴CD=AB=9,∠D=90°,
∴DE=9-6=3,
∴AE=
=
=5;
(2)①若∠EPA=90°,t=6;
②若∠PEA=90°,(6-t)2+42+52=(9-t)2,
解得t=
.
综上所述,当t=6或t=
时,△PAE为直角三角形;
(3)假设存在.
∵EA平分∠PED,
∴∠PEA=∠DEA.
∵CD∥AB,
∴∠DEA=∠EAP,
∴∠PEA=∠EAP,
∴PE=PA,
∴(6-t)2+42=(9-t)2,
解得t=
.
∴满足条件的t存在,此时t=
.
∴CD=AB=9,∠D=90°,
∴DE=9-6=3,
∴AE=
| DE2+AD2 |
| 32+42 |
(2)①若∠EPA=90°,t=6;
②若∠PEA=90°,(6-t)2+42+52=(9-t)2,
解得t=
| 2 |
| 3 |
综上所述,当t=6或t=
| 2 |
| 3 |
(3)假设存在.
∵EA平分∠PED,
∴∠PEA=∠DEA.
∵CD∥AB,
∴∠DEA=∠EAP,
∴∠PEA=∠EAP,
∴PE=PA,
∴(6-t)2+42=(9-t)2,
解得t=
| 29 |
| 6 |
∴满足条件的t存在,此时t=
| 29 |
| 6 |
看了 如图,矩形ABCD中,AB=...的网友还看了以下:
如图1,在△ABC中,∠A=30°,点P从点A出发以2cm/s的速度沿折线A-C-B运动,点Q从点 2020-05-16 …
下面属于商品证券的有( )。A.提货单B.运货单 C.仓库栈单D.存款单 F.取暂苗 2020-05-21 …
下面属于商品证券的有( )。 A.提货单B.运货单 C.仓库栈单D.存款单 F.取暂苗 2020-05-21 …
A、B两物体分别在水平拉力作用下沿水平面做匀速直线运动,如果B所受的拉力是A的3倍,A的运动速度是 2020-05-23 …
下面属于商品证券的有( )。 A.提货单 B.运货单 C.仓库栈单 D.存款单 2020-05-30 …
求一个关于瞬间速度和运动平均的问题假如有a和b是完全相同的物体,它们在完全相同的地方向同一方向运动 2020-08-02 …
如图,数轴上点A,B表示的数分别为-40,50.现有一动点P以2个单位每秒的速度从点A向B运动,另一 2020-10-30 …
下列单据中,经审核无误后可以作为编制记账凭证依据的是A.填制完毕的工资计算单B.运费发票C.银行转来 2020-11-28 …
如图,在长方形ABCD中,AB=6,CB=8,点P与点Q分别是AB、CB边上的动点,点P与点Q同时出 2020-12-03 …
如图,抛物线y=-1/2(x-5/2)²+9/8与X轴相交于A、B两点,与Y轴相交于C点,过点C做C 2021-01-11 …