早教吧作业答案频道 -->数学-->
我们知道:圆周角的度数等于它所对弧上的圆心角度数的一半.(1)请你分”圆周角的一边过圆心“、”圆心在圆周角的内部“、”圆心在圆周角的外部“3种情况,分别结合图①、②、③
题目详情
我们知道:圆周角的度数等于它所对弧上的圆心角度数的一半.
(1)请你分”圆周角的一边过圆心“、”圆心在圆周角的内部“、”圆心在圆周角的外部“3种情况,分别结合图①、②、③证明上述结论;
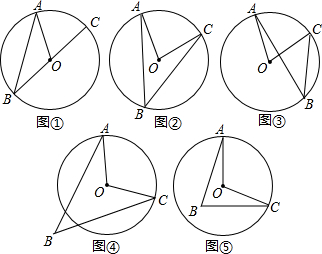
(2)证明上述结论,运用的数学思想方法有:___.
(3)我们把“顶点在圆外的角”称之为“圆外角”,把“顶点在圆内的角”称之为“圆内角”,“圆外角”或“圆内角”是否依然等于“它所对弧上的圆心角度数的一半”?请你分别结合图④、⑤对你的结论加以说明.
(1)请你分”圆周角的一边过圆心“、”圆心在圆周角的内部“、”圆心在圆周角的外部“3种情况,分别结合图①、②、③证明上述结论;

(2)证明上述结论,运用的数学思想方法有:___.
(3)我们把“顶点在圆外的角”称之为“圆外角”,把“顶点在圆内的角”称之为“圆内角”,“圆外角”或“圆内角”是否依然等于“它所对弧上的圆心角度数的一半”?请你分别结合图④、⑤对你的结论加以说明.
▼优质解答
答案和解析
 (1)在图①中,∵OA=OB,
(1)在图①中,∵OA=OB,
∴∠A=∠B,
又∵∠AOC=∠A+∠B,
∴∠B=
∠AOC;
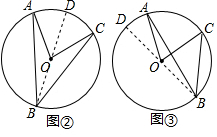
在图②中,作直径BD,同①可得∠ABD=
∠AOD,∠CBD=
∠COD,
则∠ABC=
∠AOC;
在图③中,作直径BD.
同理∠CBD=
∠COD,∠ABD=
∠AOD,
∴∠ABC=∠CBD-∠ABD=
∠COD-
∠AOD=
(∠COD-∠AOD)=
∠AOC;
(2)运用了分类讨论思想.
故答案是:分类讨论;
(3)圆外角”或“圆内角”不等于“它所对弧上的圆心角度数的一半”.
如图④.
连接CD.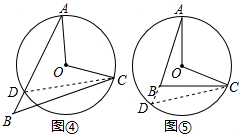
根据(1)可得∠ADC=
∠AOC,
又∵∠ADC>∠B,
∴∠B<
∠AOC;
在图⑤中,延长AB交圆于点D,连接CD.
∵∠D=
∠AOC,
又∵∠D<∠ABC,
∴∠ABC>
∠AOC.
 (1)在图①中,∵OA=OB,
(1)在图①中,∵OA=OB,∴∠A=∠B,
又∵∠AOC=∠A+∠B,
∴∠B=
| 1 |
| 2 |
在图②中,作直径BD,同①可得∠ABD=
| 1 |
| 2 |
| 1 |
| 2 |
则∠ABC=
| 1 |
| 2 |
在图③中,作直径BD.
同理∠CBD=
| 1 |
| 2 |
| 1 |
| 2 |
∴∠ABC=∠CBD-∠ABD=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
(2)运用了分类讨论思想.
故答案是:分类讨论;
(3)圆外角”或“圆内角”不等于“它所对弧上的圆心角度数的一半”.
如图④.
连接CD.

根据(1)可得∠ADC=
| 1 |
| 2 |
又∵∠ADC>∠B,
∴∠B<
| 1 |
| 2 |
在图⑤中,延长AB交圆于点D,连接CD.
∵∠D=
| 1 |
| 2 |
又∵∠D<∠ABC,
∴∠ABC>
| 1 |
| 2 |
看了 我们知道:圆周角的度数等于它...的网友还看了以下:
数轴上不同的两个点表示的数,边的点表示的数总比边的点表示的数大.于是有:负数0,0正数,负数正数. 2020-05-13 …
三道很难的数学题1:已知圆M:x^2+(y-2)^2=1,Q点是x轴上的一动点,QA,QB分别切圆 2020-06-13 …
李明到某影剧城游玩,看见一圆弧形门如图所示,李明想知道这扇门的相关数据.于是她从景点管理人员处打听 2020-06-15 …
(1)请将1-15填人图1中的15个圆圈中,使得除了第一行外每个圆圈内的数都等于与其肩膀上两个圆圈 2020-06-22 …
给出锐角△ABC,以AB为直径的圆与AB边的高CC′及其延长线交于M,N.以AC为直径的圆与AC边 2020-07-08 …
关于圆的题1.过A,B两点作圆,使圆心在AB上,这样可以作_____个圆.2.三角形的外心到三角形 2020-07-30 …
已知圆C的极坐标方程为ρ=4cosθ-6sinθ,直线l的参数方程为x=4+tcosθy=tsin 2020-07-31 …
在平面直角坐标系xOy中,圆C的参数方程为x=4cosθy=4sinθ(θ为参数).直线l经过点P 2020-08-01 …
(2010•河池模拟)小明发现家中电熨斗铭牌上的某个数据模糊不清(如右表).他很想知道铭牌上的这个数 2020-11-13 …
圆周角:(1)定理:一条弧所对的圆周角.(2)推论:①圆周角的度数等于它所对弧的度数的.②同弧或等弧 2020-12-23 …