早教吧作业答案频道 -->数学-->
探究与发现:如图①,在Rt△ABC中,∠BAC=90°,AB=AC,点D在底边BC上,AE=AD,连结DE.(1)当∠BAD=60°时,求∠CDE的度数;(2)当点D在BC(点B、C除外)上运动时,试猜想并探究∠BAD与∠CDE
题目详情
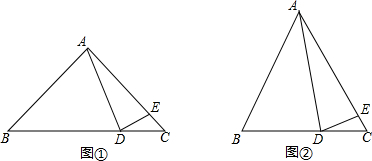
探究与发现:如图①,在Rt△ABC中,∠BAC=90°,AB=AC,点D在底边BC上,AE=AD,连结DE.
(1)当∠BAD=60°时,求∠CDE的度数;
(2)当点D在BC (点B、C除外) 上运动时,试猜想并探究∠BAD与∠CDE的数量关系;
(3)深入探究:若∠BAC≠90°,试就图②探究∠BAD与∠CDE的数量关系.
(1)当∠BAD=60°时,求∠CDE的度数;
(2)当点D在BC (点B、C除外) 上运动时,试猜想并探究∠BAD与∠CDE的数量关系;
(3)深入探究:若∠BAC≠90°,试就图②探究∠BAD与∠CDE的数量关系.

▼优质解答
答案和解析
(1)∵AB=AC,∠BAC=90°,
∴∠B=∠C=45°,
∵∠BAD=60°,
∴∠DAE=30°,
∵AD=AE,
∴∠AED=75°,
∴∠CDE=∠AED=∠C=30°;
(2)设∠BAD=x,
∴∠CAD=90°-x,
∵AE=AD,
∴∠AED=45°+
x,
∴∠CDE=
x;
(3)设∠BAD=x,∠C=y,
∵AB=AC,∠C=y,
∴∠BAC=180°-2y,
∵∠BAD=x,
∴∠DAE=y+
x,
∴∠CDE=∠AED-∠C=
x.
∴∠B=∠C=45°,
∵∠BAD=60°,
∴∠DAE=30°,
∵AD=AE,
∴∠AED=75°,
∴∠CDE=∠AED=∠C=30°;
(2)设∠BAD=x,
∴∠CAD=90°-x,
∵AE=AD,
∴∠AED=45°+
| 1 |
| 2 |
∴∠CDE=
| 1 |
| 2 |
(3)设∠BAD=x,∠C=y,
∵AB=AC,∠C=y,
∴∠BAC=180°-2y,
∵∠BAD=x,
∴∠DAE=y+
| 1 |
| 2 |
∴∠CDE=∠AED-∠C=
| 1 |
| 2 |
看了 探究与发现:如图①,在Rt△...的网友还看了以下:
如图表示酶的催化反应过程.有关叙述错误的是()A.适当增大①的浓度会提高酶促反应的速度B.如果探究底 2020-03-30 …
2014年3月,某海域发生航班失联事件,我海事救援部门用高频海洋探测仪进行海上搜救,分别在A、B两 2020-05-16 …
目前人类发射的探测器已飞出太阳系,正想更远的太空飞去.如果探测器所受外力全部消失,那没探测器将() 2020-05-17 …
发现身边的历史——我写我家写广东省东莞市高埗镇有关的,分A文和B文.A文:探究活动成果.真实的记录 2020-05-17 …
关于荨麻疹的描述,哪条不正确?A.一般都发展为慢性B.如发生在喉头粘膜,可见呼吸困难,甚至窒息C.如 2020-05-31 …
如图在△ABC中,∠C=90°,BC=8cm,AC=6cm,点Q从B出发,沿BC方向以2cm/s的 2020-06-22 …
实验探究为了探究甲状腺激素对蝌蚪发育的影响,接庄中学某兴趣小组设计了如下探究实验:(1)取两个规格 2020-07-03 …
2013年3月,某煤矿发生瓦斯爆炸,该地救援队立即赶赴现场进行救援,救援队利用生命探测仪在地面A、B 2020-11-02 …
蚂蚁是怎么样进行通讯的,某实验小组做了如下探究实验,如图:提出问题:有同学提出,蚂蚁不会发声,它们是 2020-11-10 …
火焰探测器利用什么来探测火灾的,主要是探测火焰发出的紫外光和红外光的?消防用的火焰探测器,是如何探测 2020-12-09 …