如图，抛物线y=ax2+bx+c，与x轴交于点A（-1，0），顶点坐标为（1，n），与y轴交点在（0，2）、（0，3）之间（包含端点），有下列结论：①abc>0；②4ac-b2>0；③当x=3时，y=0；④3a+b>0；⑤-1

Question

如图，抛物线y=ax²+bx+c，与x轴交于点A（-1，0），顶点坐标为（1，n），与y轴交点在（0，2）、（0，3）之间（包含端点），有下列结论：①abc>0；②4ac-b²>0；③当x=3时，y=0；④3a+b>0；⑤-1≤a≤-

(2)/(3)，；⑥(8)/(3)≤n≤4，其中正确的有（　　）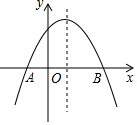

A. 1个

B. 2个

C. 3个

D. 4个

Answer 1

由函数图象可a<0，b>0，c>0，
∴abc<0，故①错误；
∵函数图象和x轴有两个交点，
∴b²-4ac>0，
即4ac-b²<0，故②错误；
∵抛物线y=ax²+bx+c与x轴交于点A（-1，0），对称轴直线是x=1，
∴该抛物线与x轴的另一个交点的坐标是（3，0），
∴当x=3时，y=0，故③正确；
根据图示知，抛物线开口方向向下，则a<0．
∵对称轴x=-(b)/(2a)=1，
∴b=-2a，
∴3a+b=3a-2a=a<0，即3a+b<0．故④错误；
∵抛物线与x轴的两个交点坐标分别是（-1，0），（3，0），
∴-1×3=-3，
(c)/(a)=-3，则a=-(c)/(3)．
∵抛物线与y轴的交点在（0，2）、（0，3）之间（包含端点），
∴2≤c≤3，
∴-1≤-(c)/(3)≤-(2)/(3)，即-1≤a≤(2)/(3)．故⑤正确；
根据题意知，a=-(c)/(3)，
-(b)/(2a)=1，
∴b=-2a=(2)/(3)，
∴n=a+b+c=(4)/(3)c．
∵2≤c≤3，(8)/(3)≤(4)/(3)c≤4，(8)/(3)≤n≤4．故⑥正确；
综上所述，正确的说法有③⑤⑥．
故选D．