如图，正方形ABCD中，AB=6，点E在边CD上，且CE=2DE．将△ADE沿AE对折至△AFE，延长EF交边BC于点G，连结AG、CF．下列结论：①△ABG≌△AFG；②BG=GC；③EG=DE+BG；④AG∥CF；⑤S△FGC=3.6．其中正确结论

Question

如图，正方形ABCD中，AB=6，点E在边CD上，且CE=2DE．将△ADE沿AE对折至△AFE，延长EF交边BC于点G，连结AG、CF．下列结论：①△ABG≌△AFG；②BG=GC；③EG=DE+BG；④AG∥CF；⑤S_△FGC=3.6．其中正确结论的个数是（　　）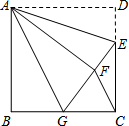

A. 2

B. 3

C. 4

D. 5

Answer 1

∵正方形ABCD的边长为6，CE=2DE，
∴DE=2，EC=4，
∵把△ADE沿AE折叠使△ADE落在△AFE的位置，
∴AF=AD=6，EF=ED=2，∠AFE=∠D=90°，∠FAE=∠DAE，
在Rt△ABG和Rt△AFG中

AB=AF

AG=AG

，
∴Rt△ABG≌Rt△AFG（HL），
∴GB=GF，∠BAG=∠FAG，
∴∠GAE=∠FAE+∠FAG=(1)/(2)∠BAD=45°，所以①正确；
设BG=x，则GF=x，C=BC-BG=6-x，
在Rt△CGE中，GE=x+2，EC=4，CG=6-x，
∵CG²+CE²=GE²，
∴（6-x）²+4²=（x+2）²，解得x=3，
∴BG=3，CG=6-3=3
∴BG=CG，所以②正确；
∵EF=ED，GB=GF，
∴GE=GF+EF=BG+DE，所以③正确；
∵GF=GC，
∴∠GFC=∠GCF，
又∵Rt△ABG≌Rt△AFG，
∴∠AGB=∠AGF，
而∠BGF=∠GFC+∠GCF，
∴∠AGB+∠AGF=∠GFC+∠GCF，
∴∠AGB=∠GCF，
∴CF∥AG，所以④正确；
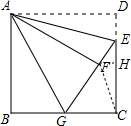
过F作FH⊥DC
∵BC⊥DH，
∴FH∥GC，
∴△EFH∽△EGC，
∴(EH)/(GC)=(EF)/(EG)，
EF=DE=2，GF=3，
∴EG=5，
∴△EFH∽△EGC，
∴相似比为：(EH)/(GC)=(EF)/(EG)=(2)/(5)，
∴S_△FGC=S_△GCE-S_△FEC=(1)/(2)×3×4-(1)/(2)×4×（ (2)/(5)×3）=(18)/(5)=3.6，所以⑤正确．
故正确的有①②③④⑤，
故选：D．