早教吧作业答案频道 -->数学-->
下列条件能判断△ABC一定为钝角三角形的是①sinA+cosA=15②AB•BC>0③b=3,c=3
题目详情
下列条件能判断△ABC一定为钝角三角形的是___
①sinA+cosA=
②
•
>0
③b=3,c=3
,B=30°
④tanA+tanB+tanC>0.
①sinA+cosA=
| 1 |
| 5 |
②
| |
| AB |
| |
| BC |
③b=3,c=3
| | 3 |
④tanA+tanB+tanC>0.
▼优质解答
答案和解析
对于①,由sinA+cosA=
,两边平方得,2sinAcosA=-
,∴A为钝角,
故①能判断△ABC一定为钝角三角形;
对于②,由
•
>0,如图,
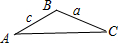
可得ac•cos(π-B)=-ac•cosB>0,则cosB<0,
∴B为钝角,故②能判断△ABC一定为钝角三角形;
③由b=3,c=3
,B=30°,得
=
,得sinC=
则C=60°或C=120°,当C=60°时,△ABC为直角三角形;
④∵tanA+tanB=tan(A+B)(1-tanAtanB),
∴tanA+tanB+tanC=tan(A+B)(1-tanAtanB)+tanC=tanAtanBtanC>0,
∴A,B,C是△ABC的内角,故内角都是锐角,△ABC为锐角三角形.
故答案为:①②.
| 1 |
| 5 |
| 24 |
| 25 |
故①能判断△ABC一定为钝角三角形;
对于②,由
| AB |
| BC |

可得ac•cos(π-B)=-ac•cosB>0,则cosB<0,
∴B为钝角,故②能判断△ABC一定为钝角三角形;
③由b=3,c=3
| 3 |
| 3 |
| sin30° |
3
| ||
| sinC |
| ||
| 2 |
则C=60°或C=120°,当C=60°时,△ABC为直角三角形;
④∵tanA+tanB=tan(A+B)(1-tanAtanB),
∴tanA+tanB+tanC=tan(A+B)(1-tanAtanB)+tanC=tanAtanBtanC>0,
∴A,B,C是△ABC的内角,故内角都是锐角,△ABC为锐角三角形.
故答案为:①②.
看了 下列条件能判断△ABC一定为...的网友还看了以下:
因式分解1)已知x^2-x+1是mx^3+nx^2+1因式,其中m,n都是整数,那么m,n的值分别 2020-05-17 …
一道二项式的题1设A=3^7+C(2,7)·3^5+C(4,7)·3^3+C(6,7)·3,B=C 2020-05-21 …
某同学的座位号为(3,5),那么该同学的所坐位置是()A.第3排第5列B.第5排第3列C.第3列第 2020-06-11 …
下列多项式相乘的结果是a2-a-6的是()A.(a-2)(a+3)B.(a+2)(a-3)C.(a 2020-07-27 …
二维数组A中,每个数据元素占4个字节,行下标从0到4,列下标从0到5,按行优先存储时元素A[3][ 2020-07-29 …
已知A、B是直线y=0与函数f(x)=2cos^2wx/2+cos(wx+派/3)-1(w>0)图 2020-07-30 …
一道因式分解难题,分解因式a^3(b-c)+b^3(c-a)+c^3(a-b).分析这是一个关于a 2020-08-02 …
将正整数依次按如表规律排成4列,根据表中的排列规律,数2016应在()第1列第2列第3列第4列第1行 2020-11-08 …
VBA问题,对worksheet行列取值的问题.对worksheet行列取值的理解已知变量ws代表某 2020-12-14 …
下列四组数分别是四名同学在同一张日历的某一列上各圈到的四个数,其中错误的一组数是()A.(7,14, 2020-12-24 …