早教吧作业答案频道 -->数学-->
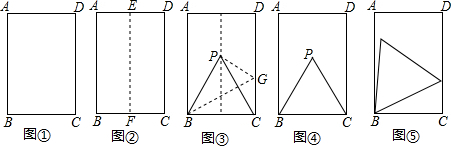
折纸的思考.操作体验用一张矩形纸片折等边三角形.第一步,对折矩形纸片ABCD(AB>BC)(图①),使AB与DC重合,得到折痕EF,把纸片展平(图②).第二步,如图③,再一次折叠纸
题目详情
折纸的思考.
【操作体验】
用一张矩形纸片折等边三角形.
第一步,对折矩形纸片ABCD(AB>BC)(图①),使AB与DC重合,得到折痕EF,把纸片展平(图②).
第二步,如图③,再一次折叠纸片,使点C落在EF上的P处,并使折痕经过点B,得到折痕BG,折出PB,PC,得到△PBC.
(1)说明△PBC是等边三角形.
【数学思考】
(2)如图④,小明画出了图③的矩形ABCD和等边三角形PBC,他发现,在矩形ABCD中把△PBC经过图形变化,可以得到图⑤中的更大的等边三角形,请描述图形变化的过程.
(3)已知矩形一边长为3cm,另一边长为a cm,对于每一个确定的a的值,在矩形中都能画出最大的等边三角形,请画出不同情形的示意图,并写出对应的a的取值范围.
【问题解决】
(4)用一张正方形铁片剪一个直角边长分别为4cm和1cm的直角三角形铁片,所需正方形铁片的边长的最小值为___cm.
【操作体验】
用一张矩形纸片折等边三角形.
第一步,对折矩形纸片ABCD(AB>BC)(图①),使AB与DC重合,得到折痕EF,把纸片展平(图②).
第二步,如图③,再一次折叠纸片,使点C落在EF上的P处,并使折痕经过点B,得到折痕BG,折出PB,PC,得到△PBC.
(1)说明△PBC是等边三角形.
【数学思考】
(2)如图④,小明画出了图③的矩形ABCD和等边三角形PBC,他发现,在矩形ABCD中把△PBC经过图形变化,可以得到图⑤中的更大的等边三角形,请描述图形变化的过程.
(3)已知矩形一边长为3cm,另一边长为a cm,对于每一个确定的a的值,在矩形中都能画出最大的等边三角形,请画出不同情形的示意图,并写出对应的a的取值范围.
【问题解决】
(4)用一张正方形铁片剪一个直角边长分别为4cm和1cm的直角三角形铁片,所需正方形铁片的边长的最小值为___cm.

▼优质解答
答案和解析
(1)证明:由折叠的性质得:EF是BC的垂直平分线,BG是PC的垂直平分线,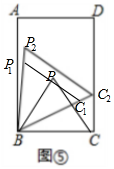
∴PB=PC,PB=CB,
∴PB=PC=CB,
∴△PBC是等边三角形.
(2) 以
点B为中心,在矩形ABCD中把△PBC逆时针方向旋转适当的角度,得到△P1BC1;
再以点B为位似中心,将△△P1BC1放大,使点C1的对称点C2落在CD上,得到△P2BC2;
如图⑤所示;
(3) 本题答案不唯一,举例如图⑥所示;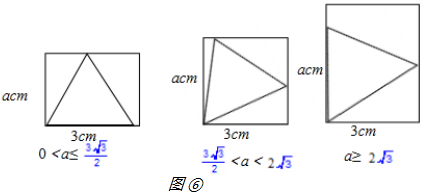
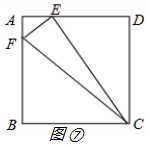
(4) 如图⑦所示:
△CEF是直角三角形,∠CEF=90°,CE=4,EF=1,
∴∠AEF+∠CED=90°,
∵四边形ABCD是正方形,
∴∠A=∠D=90°,AD=CD,
∴∠DCE+∠CED=90°,
∴∠AEF=∠DCE,
∴△AEF∽△DCE,
∴
=
=
,
设AE=x,则AD=CD=4x,
∴DE=AD-AE=3x,
在Rt△CDE中,由勾股定理得:(3x)2+(4x)2=42,
解得:x=
,
∴AD=4×
=
;
故答案为:
.

∴PB=PC,PB=CB,
∴PB=PC=CB,
∴△PBC是等边三角形.
(2) 以
3
| ||
| 2 |
再以点B为位似中心,将△△P1BC1放大,使点C1的对称点C2落在CD上,得到△P2BC2;
如图⑤所示;
(3) 本题答案不唯一,举例如图⑥所示;

(4) 如图⑦所示:
△CEF是直角三角形,∠CEF=90°,CE=4,EF=1,
∴∠AEF+∠CED=90°,
∵四边形ABCD是正方形,
∴∠A=∠D=90°,AD=CD,
∴∠DCE+∠CED=90°,
∴∠AEF=∠DCE,
∴△AEF∽△DCE,
∴
| AE |
| DC |
| EF |
| CE |
| 1 |
| 4 |

设AE=x,则AD=CD=4x,
∴DE=AD-AE=3x,
在Rt△CDE中,由勾股定理得:(3x)2+(4x)2=42,
解得:x=
| 4 |
| 5 |
∴AD=4×
| 4 |
| 5 |
| 16 |
| 5 |
故答案为:
| 16 |
| 5 |
看了 折纸的思考.操作体验用一张矩...的网友还看了以下:
一张长12的正方形纸片剪去两个相同的小矩形得到一个E形图案设小矩形的长与宽分别为XY剩余部分的面积 2020-04-09 …
矩形ABCD中,AB=3,BC=4,E是BC上一点,DF⊥AE于F,设AE的长为x,DF的长为y, 2020-05-17 …
剪力图和弯矩图.不求画图,只求剪力方程和弯力方程怎么列.在图中,外伸梁上均布载荷的集度为q=3km 2020-05-17 …
杆件-受力分析-对称在材料力学中,对称梁受到对称荷载的作用,其剪力图是对称还是反对称?弯矩图式对称 2020-07-08 …
一张边长为16cm正方形的纸片,剪去两个面积一定且一样的小矩形得到一个“E”图案如图1所示.小矩形 2020-07-16 …
已知(E12)*A=B.对其求逆矩阵得A^-1*(E12)^-1=B^-1,为什么行变换得到的初等 2020-08-02 …
如图1是由两个长方体所组成的立体图形,图2中的长方体是图1中的两个长方体的另一种摆放形式,图①②③ 2020-08-02 …
下列叙述正确的是A.平移与旋转都表示物体(图形)运动的过程,所以平移就是旋转B.因为中心对称图形也 2020-08-03 …
.已知矩形周长为6P,将其绕其一边旋转而构成旋转体,求所得体积为最大的那个矩形的尺寸.(大学数学分析 2020-11-30 …
一张边长为16cm正方形的纸片,剪去两个面积一定且一样的小矩形得到一个“E”图案如图1.小矩形的长x 2020-12-05 …