早教吧作业答案频道 -->数学-->
在等边△ABC中,AB=2,点E是BC边上一点,∠DEF=60°,且∠DEF的两边分别与△ABC的边AB,AC交于点P,Q(点P不与点A,B重合).(1)若点E为BC中点.①当点Q与点A重合,请在图1中补全图形;②在图
题目详情
在等边△ABC中,AB=2,点E是BC边上一点,∠DEF=60°,且∠DEF的两边分别与△ABC的边AB,AC交于点P,Q(点P不与点A,B重合).
(1)若点E为BC中点.
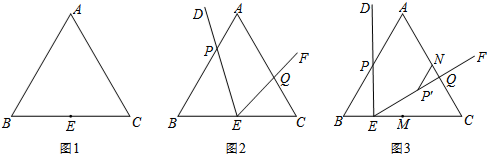
①当点Q与点A重合,请在图1中补全图形;
②在图2中,将∠DEF绕着点E旋转,设BP的长为x,CQ的长为y,求y与x的函数关系式,并写出自变量x的取值范围;
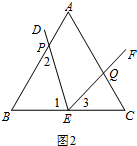
(2)如图3,当点P为AB的中点时,点M,N分别为BC,AC的中点,在EF上截取EP′=EP,连接NP′.请你判断线段NP′与ME的数量关系,并说明理由.
(1)若点E为BC中点.
①当点Q与点A重合,请在图1中补全图形;
②在图2中,将∠DEF绕着点E旋转,设BP的长为x,CQ的长为y,求y与x的函数关系式,并写出自变量x的取值范围;
(2)如图3,当点P为AB的中点时,点M,N分别为BC,AC的中点,在EF上截取EP′=EP,连接NP′.请你判断线段NP′与ME的数量关系,并说明理由.

▼优质解答
答案和解析
(1)①补全图形,如图1所示,
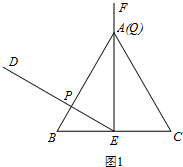
②如图2,
∵等边△ABC,
∴∠B=∠C=∠DEF=60°,AB=BC=AC=2.
∴∠1+∠2=∠1+∠3=120°.
∴∠2=∠3.
∴△PBE∽△ECQ.
∴
=
.
∵点E为BC的中点,
∴BE=EC=1,
∵BP的长为x,CQ的长为y,
∴
=
.
即y=
.
自变量x的取值范围是:
≤x<2.
(2)如图3,
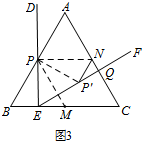
答:NP′=ME
证明:连接PM,PN,PP′.
∵P,M,N分别是AB,BC,AC的中点,
∴PN∥BC,PN=
BC,PM∥AC,PM=
AC.
∴四边形PMCN为平行四边形,
∵△ABC是等边三角形,
∴BC=AC,∠C=60°.
∴PM=PN,∠NPM=∠C=60°.
∵EP=EP′,∠PEP′=60°,
∴△PEP′是等边三角形.
∴∠EPP′=60°,PE=PP′.
∴∠EPP′=∠NPM.
∴∠EPM=∠NPP′.
∴△EPM≌△NPP′.
∴NP′=ME.

②如图2,

∵等边△ABC,
∴∠B=∠C=∠DEF=60°,AB=BC=AC=2.
∴∠1+∠2=∠1+∠3=120°.
∴∠2=∠3.
∴△PBE∽△ECQ.
∴
| BP |
| EC |
| BE |
| CQ |
∵点E为BC的中点,
∴BE=EC=1,
∵BP的长为x,CQ的长为y,
∴
| x |
| 1 |
| 1 |
| y |
即y=
| 1 |
| x |
自变量x的取值范围是:
| 1 |
| 2 |
(2)如图3,

答:NP′=ME
证明:连接PM,PN,PP′.
∵P,M,N分别是AB,BC,AC的中点,
∴PN∥BC,PN=
| 1 |
| 2 |
| 1 |
| 2 |
∴四边形PMCN为平行四边形,
∵△ABC是等边三角形,
∴BC=AC,∠C=60°.
∴PM=PN,∠NPM=∠C=60°.
∵EP=EP′,∠PEP′=60°,
∴△PEP′是等边三角形.
∴∠EPP′=60°,PE=PP′.
∴∠EPP′=∠NPM.
∴∠EPM=∠NPP′.
∴△EPM≌△NPP′.
∴NP′=ME.
看了 在等边△ABC中,AB=2,...的网友还看了以下:
数轴上点A对应的数是-1,B点对应的数是1,点A、B、C分别以1单位一秒,三单位一秒,四单位一秒在数 2020-03-30 …
数轴上点A对应的数是-1,B点对应的数是1,点A、B、C分别以1单位一秒,三单位一秒,四单位一秒在数 2020-03-30 …
从某个角度看到骰子的三个面上是1点、2点和3点,与这三个面分别平行的面分别是4点、5点和6点,如果 2020-06-24 …
古代时间表述问题,每更分五点的话,每点就是24分钟,三更是23点到1点的话,三更三点应该是23点加 2020-06-30 …
某军事行动中,对军队部署的方位,采用钟代码的方式来表示.例如,北偏东30度方向45千米的位置,与钟 2020-07-05 …
一道有关骰子的概率问题设有两颗骰子任意投掷一次,两颗都出现1点的概率是?分别出现1点和2点的概率是 2020-07-06 …
已知点P和点Q是曲线y=x2-2x-3上的两点,且点P的横坐标是1,点Q的横坐标是4,求:已知点P 2020-07-31 …
若∠1与∠B互为补角,∠B=∠E,那么直线AB与直线DE平行吗?直线BC与直线EF平行吗?为什么? 2020-08-02 …
数轴上点A对应的数是-1,点B对应的数是1,一只小虫甲从点B出发沿着数轴的正方向以每秒1个单位的速度 2020-11-17 …
从凌晨0:00到当日24:00点前,时钟的时针和分针一共会有次在一直线上;其中在下午1点到下午2点间 2020-12-03 …