如图，已知直线y=k1x+b与x轴，y轴相交于P，Q两点，则y=k2x的图象相交于A（-2，m），B（1，n）两点，连接OA，OB，给出下列结论：①k1k2<0；②m+12n=0；③S△AOP=S△BOQ；④不等式k1x+b>k2x的解集在

Question

如图，已知直线y=k₁x+b与x轴，y轴相交于P，Q两点，则y=

(k2)/(x)的图象相交于A（-2，m），B（1，n）两点，连接OA，OB，给出下列结论：①k₁k₂<0；②m+(1)/(2)n=0；③S_△AOP=S_△BOQ；④不等式k₁x+b>(k2)/(x)的解集在x<-2或0<x<1，其中正确的结论是（　　）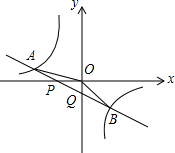

A. ②③④

B. ①②③④

C. ③④

D. ②③

Answer 1

由图象知，k₁<0，k₂<0，
∴k₁k₂>0，故①错误；
把A（-2，m）、B（1，n）代入y=(k2)/(x)中得-2m=n，
∴m+(1)/(2)n=0，故②正确；
把A（-2，m）、B（1，n）代入y=k₁x+b得

m=-2k1+b

n=k1+b

，
∴

k1=(n-m)/(3)

b=(2n+m)/(3)

，
∵-2m=n，
∴y=-mx-m，
∵已知直线y=k₁x+b与x轴、y轴相交于P、Q两点，
∴P（-1，0），Q（0，-m），
∴OP=1，OQ=m，
∴S_△AOP=(1)/(2)m，S_△BOQ=(1)/(2)m，
∴S_△AOP=S_△BOQ；故③正确；
由图象知不等式k₁x+b>(k2)/(x)的解集是x<-2或0<x<1，故④正确；
故选A．