早教吧作业答案频道 -->数学-->
已知抛物线G1:y=a(x-h)2+2的对称轴为x=-1,且经过原点.(1)求抛物线G1的表达式;(2)将抛物线G1先沿x轴翻折,再向左平移1个单位后,与x轴分别交于A,B两点(点A在点B的左侧),与y轴
题目详情
已知抛物线G1:y=a(x-h)2+2的对称轴为x=-1,且经过原点.
(1)求抛物线G1的表达式;
(2)将抛物线G1先沿x轴翻折,再向左平移1个单位后,与x轴分别交于A,B两点(点A在点B的左侧),与y轴交于C点,求A点的坐标;
(3)记抛物线在点A,C之间的部分为图象G2(包含A,C两点),如果直线m:y=kx-2与图象G2只有一个公共点,请结合函数图象,求直线m与抛物线G2的对称轴交点的纵坐标t的值或范围.

(1)求抛物线G1的表达式;
(2)将抛物线G1先沿x轴翻折,再向左平移1个单位后,与x轴分别交于A,B两点(点A在点B的左侧),与y轴交于C点,求A点的坐标;
(3)记抛物线在点A,C之间的部分为图象G2(包含A,C两点),如果直线m:y=kx-2与图象G2只有一个公共点,请结合函数图象,求直线m与抛物线G2的对称轴交点的纵坐标t的值或范围.
▼优质解答
答案和解析
(1)∵抛物线G1:y=a(x-h)2+2的对称轴为x=-1,
∴y=a(x+1)2+2,
∵抛物线y=a(x+1)2+2经过原点,
∴a(0+1)2+2=0.
解得 a=-2,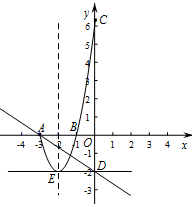
∴抛物线G1的表达式为y=-2(x+1)2+2=-2x2-4x;
(2)由题意得,抛物线G2的表达式为y=2(x+1+1)2-2=2x2+8x+6.
∴当y=0时,x=-1或-3.
∴A(-3,0);
(3)由题意得,直线m:y=kx-2交y轴于点D(0,-2),
由抛物线G2的解析式y=2x2+8x+6,得到顶点E(-2,-2),
当直线y=kx-2过E(-2,-2)时与图象G2只有一个公共点,此时t=-2,
当直线y=kx-2过A(-3,0)时
把x=-3代入y=kx-2,k=-
,
∴y=-
x-2,
把x=-2代入y=-
x-2,
∴y=-
,即t=-
,
∴结合图象可知t=-2或t>-
.
∴y=a(x+1)2+2,
∵抛物线y=a(x+1)2+2经过原点,
∴a(0+1)2+2=0.
解得 a=-2,

∴抛物线G1的表达式为y=-2(x+1)2+2=-2x2-4x;
(2)由题意得,抛物线G2的表达式为y=2(x+1+1)2-2=2x2+8x+6.
∴当y=0时,x=-1或-3.
∴A(-3,0);
(3)由题意得,直线m:y=kx-2交y轴于点D(0,-2),
由抛物线G2的解析式y=2x2+8x+6,得到顶点E(-2,-2),
当直线y=kx-2过E(-2,-2)时与图象G2只有一个公共点,此时t=-2,
当直线y=kx-2过A(-3,0)时
把x=-3代入y=kx-2,k=-
| 2 |
| 3 |
∴y=-
| 2 |
| 3 |
把x=-2代入y=-
| 2 |
| 3 |
∴y=-
| 2 |
| 3 |
| 2 |
| 3 |
∴结合图象可知t=-2或t>-
| 2 |
| 3 |
看了 已知抛物线G1:y=a(x-...的网友还看了以下:
两平面镜如图所示放置,有一点光源S在图示位置,从S发出的一条光线经两平面镜P,Q反射后,反射光线还 2020-05-20 …
试证明两平面镜夹角为θ,入射到它上面的光线经两次反射后,其出射光线与入射光线的夹角为2θ,也就是说 2020-05-23 …
如图所示,两块平面镜相交成60°角,一束光线AO射到平面镜MP上,光线经两平面镜反射后与AO重合, 2020-06-15 …
如图所示,两块平面镜MP、PN相交,夹角为60°,一束光线AO斜射到平面镜MP上,光线经两平面镜反 2020-07-13 …
(1)自行车尾灯是由互相垂直的小平面镜组成的角反射器,请你在图甲中画出入射光线经两个平面反射的光路 2020-07-20 …
两平面镜间夹角为θ,从任意方向入射到一个镜面的光线经两个镜面上两次反射后,出射线与入射线之间的夹角为 2020-11-07 …
如图所示,要使入射光线经两次反射后沿原路返回,则α角为()A.10°B.20°C.70°D.无法确定 2020-11-25 …
自行车的“尾灯”是由许多很小的角反射器组成的.角反射器其实就是两个相互垂直的平面镜,如图所示.请在图 2020-12-07 …
(2005•泰州)自行车的“尾灯”是由许多很小的角反射器组成的.角反射器其实就是两个相互垂直的平面镜 2021-01-12 …
(1)自行车的“尾灯”是由许多很小的角反射器组成的.角反射器其实就是两个相互垂直的平面镜,如图1所示 2021-01-12 …