早教吧作业答案频道 -->数学-->
在△ABC中,以AB为斜边,作直角△ABD,使点D落在△ABC内,∠ADB=90°.(1)如图1,若AB=AC,∠DBA=60°,AD=73,点P、M分别为BC、AB边的中点,连接PM,求线段PM的长;(2)如图2,若AB=AC,把△ABD绕
题目详情
在△ABC中,以AB为斜边,作直角△ABD,使点D落在△ABC内,∠ADB=90°.
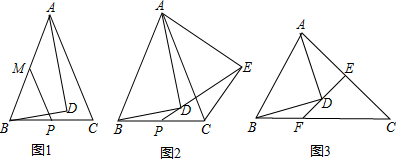
(1)如图1,若AB=AC,∠DBA=60°,AD=7
,点P、M分别为BC、AB边的中点,连接PM,求线段PM的长;
(2)如图2,若AB=AC,把△ABD绕点A逆时针旋转一定角度,得到△ACE,连接ED并延长交BC于点P,求证:BP=CP;
(3)如图3,若AD=BD,过点D的直线交AC于点E,交BC于点F,EF⊥AC,且AE=EC,请直接写出线段BF、FC、AD之间的关系(不需要证明).
(1)如图1,若AB=AC,∠DBA=60°,AD=7
| 3 |
(2)如图2,若AB=AC,把△ABD绕点A逆时针旋转一定角度,得到△ACE,连接ED并延长交BC于点P,求证:BP=CP;
(3)如图3,若AD=BD,过点D的直线交AC于点E,交BC于点F,EF⊥AC,且AE=EC,请直接写出线段BF、FC、AD之间的关系(不需要证明).

▼优质解答
答案和解析
(1) 如图1中,
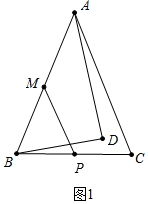
∵∠ADB=90°,∠DBA=60°,AD=7
,
∴∠BAD=30°,
∴AB=2BD,设BD=a,则AB=2a,
∵AB2=BD2+AD2,
∴(2a)2=a2+(7
)2,
∴a=7,
∴AB=AC=14,
∵AM=MB,PB=PC,
∴PM=
AC=7.
(2)证明:如图2中,在ED上截取EQ=DP,连接CQ.
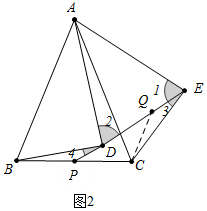
∵AD=AE,
∴∠1=∠2,
∵∠ADB=∠AEC=90°,
∴∠1+∠3=90°,∠2+∠4=90°,
∴∠3=∠4,
∵BD=EC,
∴△EQC≌△DPB,
∴CQ=BP,∠QCE=∠DBP,
∵∠CQP=∠3+∠QCE,∠CPQ=∠4+∠DBP,
∴∠CQP=∠CPQ,
∴CQ=PC,
∴PB=PC.
(3)结论:2AD2=FB2+CF2.
理由:如图3中,连接AF交BD于N.
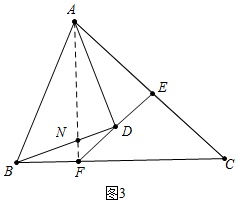
∵∠ADB=90°,DA=DB,
∴∠DBA=∠DAB=45°,AB=
AD,
∵∠AND=∠BNF,∠ADN=∠BFN=90°,
∴△AND∽△BNF,
∴
=
,
∴
=
,∵∠ANB=∠DNF,
∴△ANB∽△DNF,
∴∠DFN=∠ABD=45°,
∵FE⊥AC,AE=EC,
∴FA=FC,∠AFE=∠CFE=45°,
∴∠AFC=∠AFB=90°,
∴AB2=BF2+AF2,
∴2AD2=BF2+CF2.

∵∠ADB=90°,∠DBA=60°,AD=7
| 3 |
∴∠BAD=30°,
∴AB=2BD,设BD=a,则AB=2a,
∵AB2=BD2+AD2,
∴(2a)2=a2+(7
| 3 |
∴a=7,
∴AB=AC=14,
∵AM=MB,PB=PC,
∴PM=
| 1 |
| 2 |
(2)证明:如图2中,在ED上截取EQ=DP,连接CQ.

∵AD=AE,
∴∠1=∠2,
∵∠ADB=∠AEC=90°,
∴∠1+∠3=90°,∠2+∠4=90°,
∴∠3=∠4,
∵BD=EC,
∴△EQC≌△DPB,
∴CQ=BP,∠QCE=∠DBP,
∵∠CQP=∠3+∠QCE,∠CPQ=∠4+∠DBP,
∴∠CQP=∠CPQ,
∴CQ=PC,
∴PB=PC.
(3)结论:2AD2=FB2+CF2.
理由:如图3中,连接AF交BD于N.

∵∠ADB=90°,DA=DB,
∴∠DBA=∠DAB=45°,AB=
| 2 |
∵∠AND=∠BNF,∠ADN=∠BFN=90°,
∴△AND∽△BNF,
∴
| AN |
| BN |
| DN |
| NF |
∴
| AN |
| DN |
| BN |
| NF |
∴△ANB∽△DNF,
∴∠DFN=∠ABD=45°,
∵FE⊥AC,AE=EC,
∴FA=FC,∠AFE=∠CFE=45°,
∴∠AFC=∠AFB=90°,
∴AB2=BF2+AF2,
∴2AD2=BF2+CF2.
看了 在△ABC中,以AB为斜边,...的网友还看了以下:
管理信息系统建设的结构化方法中用户必须参与原则是用户必须参与A.系统建设的各阶段工作B.系统分 2020-05-23 …
管理信息系统建设的结构化方法中用户必须参与的原则是用户必须参与()。A.系统建设中各阶段工作B. 2020-05-23 …
管理信息系统建设的结构化方法中用户必须参与原则是用户必须参与()。A.系统建设中各阶段工作B.系 2020-05-23 …
管理信息系统建设的结构化方法中用户必须参与的原则是拥护并参与()。A.系统建设中各阶段工作B.系 2020-05-24 …
● 关于无线局域网,下面叙述中正确的是 (64) 。 (64)A. 802.11a 和802.11b 2020-05-25 …
管理信息系统建设的结构化方法中,用户参与的原则是用户必须参与(66)。A.系统建设中各阶段工作B.系 2020-05-26 …
关于无线局域网,下面叙述中正确的是().A.802.11a和802.11b都可以在2.4GHz频段工 2020-05-26 …
伪造的货币是指()的假币。A.采用各种造假手段制作B.仿照真币的图案、形状、色彩等采用各种手段制作C 2020-05-27 …
管理信息系统建设的结构化方法中,用户参与的原则是用户必须参与( )。A.系统建设中各阶段工作B.系 2020-05-27 …
已知线段AB=10,点P在线段AB上,且AP=6,以A为圆心AP为半径作⊙A,点C在⊙A上,以B为 2020-06-08 …