早教吧作业答案频道 -->数学-->
阅读下面的证明过程,在括号内补充推理的依据.已知:如图,∠ACE是△ABC的外角,BD平分∠ABC,CD平分∠ACE.求证:12∠A=∠D证明:∵BD平分∠ABC()∴∠1=1
题目详情
阅读下面的证明过程,在括号内补充推理的依据.
已知:如图,∠ACE是△ABC的外角,BD平分∠ABC,CD平分∠ACE.
求证:
∠A=∠D
证明:∵BD平分∠ABC(___)
∴∠1=
∠ABC(___)
同理得∠2=
∠ACE
又∵∠ACE=∠A+∠ABC(___)
∴
∠ACE=
∠A+
∠ABC(___)
即∠2=
∠A+∠1(___)
又∵∠2=∠D+∠1
∴
∠A+∠1=∠D+∠1(___)
∴
∠A=∠D.
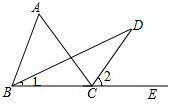
已知:如图,∠ACE是△ABC的外角,BD平分∠ABC,CD平分∠ACE.
求证:
| 1 |
| 2 |
证明:∵BD平分∠ABC(___)
∴∠1=
| 1 |
| 2 |
同理得∠2=
| 1 |
| 2 |
又∵∠ACE=∠A+∠ABC(___)
∴
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
即∠2=
| 1 |
| 2 |
又∵∠2=∠D+∠1
∴
| 1 |
| 2 |
∴
| 1 |
| 2 |

▼优质解答
答案和解析
证明:∵BD平分∠ABC(已知),
∴∠1=
∠ABC(角平分线的定义),
同理得∠2=
∠ACE.
又∵∠ACE=∠A+∠ABC(三角形外角的性质),
∴
∠ACE=
∠A+
∠ABC(等式的性质),
即∠2=
∠A+∠1(等量代换).
又∵∠2=∠D+∠1,
∴
∠A+∠1=∠D+∠1(三角形外角的性质),
∴
∠A=∠D.
故答案为:已知,角平分线的定义,三角形外角的性质,等量代换,三角形外角的性质.
∴∠1=
| 1 |
| 2 |
同理得∠2=
| 1 |
| 2 |
又∵∠ACE=∠A+∠ABC(三角形外角的性质),
∴
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
即∠2=
| 1 |
| 2 |
又∵∠2=∠D+∠1,
∴
| 1 |
| 2 |
∴
| 1 |
| 2 |
故答案为:已知,角平分线的定义,三角形外角的性质,等量代换,三角形外角的性质.
看了 阅读下面的证明过程,在括号内...的网友还看了以下:
求一数列.高2.a(n+1)=2an/2an+1已知a1=1a(n+1)=2an/2an+1求数列 2020-04-25 …
设A={a,b,c,d},B={0,1,2}设|A|=m,|B|=n,分别说明存在单射、满射、双射 2020-05-14 …
实数a,b在数轴上的位置如下图所示,化简:根号a²-根号b²+根号(a+b)²a在-1的右侧,靠近 2020-05-16 …
设f(x)={e^x+a,x>0 3x+b,x≤0.若limx→0f(x)存在,则必有(A)b-a 2020-05-17 …
五位同学的身高分别是1.42米、1.62米、1.58米、1.46米和1.52米,他们的平均身高应该 2020-06-11 …
五位同学的身高分别是1.42米、1.62米、1.58米、1.46米和1.52米,他们的平均身高应该 2020-06-11 …
符合下列条件的三角形有且只有一个的是()A.a=1,b=2,c=3B.a=1,b=2,∠A=30° 2020-06-12 …
设矩阵A,B满足A=E(1,3)E(5(-2))BE(3,2(1/2)),则有A.B=E(1,3) 2020-06-28 …
估计√8-1的值在A0---1之间B在1----2之间C在2----3之间D在3---4之间 2020-07-09 …
下列关于水的性质的叙述中,不属于物理性质的是A.常温下水是没有颜色、没有气味、没有味道的液体B.在1 2021-01-22 …