早教吧作业答案频道 -->数学-->
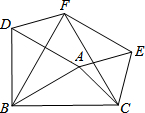
如图,在△ABC中,AB=2,AC=2,∠BAC=105°,△ABD、△ACE、△BCF都是等边三角形,则四边形AEFD的面积为.
题目详情
如图,在△ABC中,AB=2,AC=
,∠BAC=105°,△ABD、△ACE、△BCF都是等边三角形,则四边形AEFD的面积为___.
| | 2 |

▼优质解答
答案和解析
∵△ABD,△ACE都是等边三角形,
∴∠DAB=∠EAC=60°,
∵∠BAC=105°,
∴∠DAE=135°,
∵△ABD和△FBC都是等边三角形,
∴∠DBF+∠FBA=∠ABC+∠ABF=60°,
∴∠DBF=∠ABC.
在△ABC与△DBF中,
∴△ABC≌△DBF(SAS),
∴AC=DF=AE=
,
同理可证△ABC≌△EFC,
∴AB=EF=AD=2,
∴四边形DAEF是平行四边形(两组对边分别相等的四边形是平行四边形).
∴∠FDA=180°-∠DAE=45°,
∴S▱AEFD=AD•(DF•sin45°)=2×(
×
)=2.
即四边形AEFD的面积是2,
故答案为:2.
∴∠DAB=∠EAC=60°,
∵∠BAC=105°,
∴∠DAE=135°,
∵△ABD和△FBC都是等边三角形,
∴∠DBF+∠FBA=∠ABC+∠ABF=60°,
∴∠DBF=∠ABC.
在△ABC与△DBF中,
|
∴△ABC≌△DBF(SAS),
∴AC=DF=AE=
| 2 |
同理可证△ABC≌△EFC,
∴AB=EF=AD=2,
∴四边形DAEF是平行四边形(两组对边分别相等的四边形是平行四边形).
∴∠FDA=180°-∠DAE=45°,
∴S▱AEFD=AD•(DF•sin45°)=2×(
| 2 |
| ||
| 2 |
即四边形AEFD的面积是2,
故答案为:2.
看了 如图,在△ABC中,AB=2...的网友还看了以下:
A、B、C、D、E、F六种元素,其中ABCDE为短周期元素,①原子半径A<C<B<E<D②原子最外 2020-05-13 …
设一数列a,b,c,d,e,f,通过栈结构不可能不可能排成的顺序数列为()A)c,b,e,f,d, 2020-06-28 …
一个9位数abcdefghi满足:1.a+b+...+h+i=cd2.a(b+d-c)=243.( 2020-07-19 …
关于电阻决定式中L与S的含义一个边长为a,横截面积为S,电阻率为ρ的正方形导体ABCD,AB、BC 2020-07-29 …
初二相似三角形在三角形ABC中,AB=5BC=3CA=4,动点(与A.C不重合)在A.C边上,EF/ 2020-11-07 …
一个9位数abcdefghi满足:1.a+b+...+h+i=cd2.a(b+d-c)=243.(e 2020-11-19 …
如图,从A到B步行走道A→D→B需要35分钟,坐车走道A→C→D→E→B需要22.5分钟,D→E→B 2020-11-25 …
已知二叉树的前序遍历序列和中序遍历序列分别是:B,A,C,D,E,F和B,D,C,E,A,F试画出该 2020-12-05 …
求解多元一次不等式的编程47a-b-c-d-e-f-g>047b-a-c-d-e-f-g>023c- 2020-12-14 …
A+、B+、C-、D、E五种粒子(分子或离子),它们分别含10个电子,已知它们有如下转化关系:①A+ 2021-01-04 …