早教吧作业答案频道 -->数学-->
如图,∠BCA=90°,AC=BC,BE⊥CF于点E,AF⊥CF于点F,其中0°<∠ACF<45°.(1)求证:△BEC≌△CFA;(2)若AF=5,EF=8,求BE的长;(3)连接AB,取AB的中点为Q,连接QE,QF,判断△QEF的形状,并
题目详情
如图,∠BCA=90°,AC=BC,BE⊥CF于点E,AF⊥CF于点F,其中0°<∠ACF<45°.
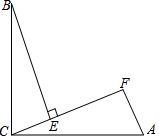
(1)求证:△BEC≌△CFA;
(2)若AF=5,EF=8,求BE的长;
(3)连接AB,取AB的中点为Q,连接QE,QF,判断△QEF的形状,并说明理由.

(1)求证:△BEC≌△CFA;
(2)若AF=5,EF=8,求BE的长;
(3)连接AB,取AB的中点为Q,连接QE,QF,判断△QEF的形状,并说明理由.
▼优质解答
答案和解析
(1)证明:∵∠BCA=∠BEC=∠F=90°,
∴∠BCE+∠B=90°,∠BCE+∠ACF=90°,
∴∠B=∠ACF,
在△BEC和△CFA中,
,
∴△BEC≌△CFA.
(2)∵△BEC≌△CFA,
∴AF=CE=5,BE=CF,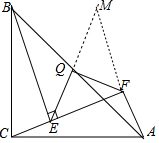
∵CF=CE+EF=5+8=13,
∴BE=13.
(3)结论:△QEF是等腰直角三角形.
理由:如图,由此EQ交AF的延长线于M.
∵BE⊥CF,AF⊥CF,
∴BE∥AM,
∴∠BEQ=∠M,
在△BQE和△AQM中,
,
∴△BQE≌△AQM,
∴EQ=QM,BE=AM=CF,
∵CE=AF,
∴FE=FM,
∴FQ⊥EM,QF=QM=QE,
∴△QEF是等腰直角三角形.
∴∠BCE+∠B=90°,∠BCE+∠ACF=90°,
∴∠B=∠ACF,
在△BEC和△CFA中,
|
∴△BEC≌△CFA.
(2)∵△BEC≌△CFA,
∴AF=CE=5,BE=CF,

∵CF=CE+EF=5+8=13,
∴BE=13.
(3)结论:△QEF是等腰直角三角形.
理由:如图,由此EQ交AF的延长线于M.
∵BE⊥CF,AF⊥CF,
∴BE∥AM,
∴∠BEQ=∠M,
在△BQE和△AQM中,
|
∴△BQE≌△AQM,
∴EQ=QM,BE=AM=CF,
∵CE=AF,
∴FE=FM,
∴FQ⊥EM,QF=QM=QE,
∴△QEF是等腰直角三角形.
看了 如图,∠BCA=90°,AC...的网友还看了以下:
小马虎计算1到2006这2006个连续整数的平均数.在求这2006个数的和时,他少算了其中的一个数 2020-06-02 …
中国古代,朝廷有时将不在户口册内且因此不纳税的人称为“盗贼”。这反映当时朝廷[]A.要求民众纳税B. 2020-11-04 …
某人站在罚球线上投篮,投中的概率为,共投了6次.(1)求此人在第3次才首次投中的概率.(2)求此人6 2020-11-16 …
高中生主题班会,谈论自己的理想,理想要结合中国的现状,是关于为国为民的理想我是理科生.就上述问题,不 2020-11-21 …
公元前5世纪中期,一位中亚成年男子不堪国内的政治迫害,为追求政治上的平等以及个人自由而奔走他乡,下列 2020-11-25 …
2011年12月12日至14日,中央经济工作会议在北京召开。会议提出,推动2012年经济社会发展,要 2020-12-20 …
中央经济工作会议2011年12月12日至14日在北京举行。会议认为,推动2012年经济社会发展,要突 2020-12-20 …
英国宪章运动的中心内容是[]A.要求集会结社权B.要求罢工权C.要求劳动权D.要求普选权 2021-01-01 …
(2014•历下区一模)2014年3月13日李克强总理在会见中外记者时用“智者求同,愚者求异”来评价 2021-01-16 …
2014年3月13日李克强总理在会见中外记者时用“智者求同,愚者求异”来评价中美关系现状.回答18- 2021-01-16 …