（本题满分12分）如图，在△ABC中，AB=AC，以AB为直径的⊙O交AC与E，交BC与D．求证：(1)、D是BC的中点；(2)、△BEC∽△ADC；(3)、若，求⊙O的半径。

Question

（本题满分12分）如图，在△ABC中，AB=AC，以AB为直径的⊙O交AC与E，交BC与D．

求证：(1)、D是BC的中点；(2)、△BEC∽△ADC；(3)、若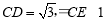 ，求⊙O的半径。

Answer 1

(1)、(2)略；(3)、3.

分 析：
(1)、根据直径所对的圆周角为直角得出AD为高线，然后根据等腰三角形的三线合一定理进行说明；(2)、根据同弧所对的圆周角相等得出∠CBE=∠CAD，然后根据∠BCE=∠ACD说明三角形相似；(3)、根据三角形相似进行求解.试题
解析：
(1)、证明：∵AB是⊙O的直径， ∴∠ADB=90° 即AD是底边BC上的高． 又∵AB=AC，∴△ABC是等腰三角形， ∴D是BC的中点(2)、证明：∵∠CBE与∠CAD是同弧所对的圆周角，∴ ∠CBE=∠CAD．又∵ ∠BCE=∠ACD， ∴△BEC∽△ADC；(3)、
由△BEC∽△ADC得：， 即CD·BC=AC·CE． ∵D是BC的中点，∴CD=BC．又 ∵AB=AC，∴CD·BC=AC·CE=BC ·BC=AB·CE 即BC=2AB·CE=12∴AB=6 ∴⊙O的半径为3……12分
考点：
圆的基本性质、三角形相似的判定与应用.