早教吧作业答案频道 -->数学-->
如图,正方形ABCD的边长为3cm,P,Q分别从B,A出发沿BC,AD方向运动,P点的运动速度是1cm/秒,Q点的运动速度是2cm/秒,连接A,P并过Q作QE⊥AP垂足为E.(1)求证:△ABP∽△QEA;(2)当运动时
题目详情
如图,正方形ABCD的边长为3cm,P,Q分别从B,A出发沿BC,AD方向运动,P点的运动速度是1cm/秒,Q点的运动速度是2cm/秒,连接A,P并过Q作QE⊥AP垂足为E.
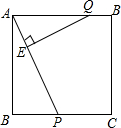
(1)求证:△ABP∽△QEA;
(2)当运动时间t为何值时,△ABP≌△QEA;
(3)设△QEA的面积为y,用运动时刻t表示△QEA的面积y(不要求考t的取值范围).(提示:解答(2)(3)时可不分先后)

(1)求证:△ABP∽△QEA;
(2)当运动时间t为何值时,△ABP≌△QEA;
(3)设△QEA的面积为y,用运动时刻t表示△QEA的面积y(不要求考t的取值范围).(提示:解答(2)(3)时可不分先后)
▼优质解答
答案和解析
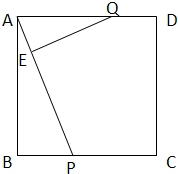 (1)证明:∵四边形ABCD为正方形;
(1)证明:∵四边形ABCD为正方形;
∴∠BAP+∠QAE=∠B=90°,
∵QE⊥AP;
∴∠QAE+∠EQA=∠AEQ=90°
∴∠BAP=∠EQA,∠B=∠AEQ;
∴△ABP∽△QEA(AA)
(2)∵△ABP≌△QEA;
∴AP=AQ(全等三角形的对应边相等);
在RT△ABP与RT△QEA中根据勾股定理得AP2=32+t2,AQ2=(2t)2
即32+t2=(2t)2
解得t1=
,t2=-
(不符合题意,舍去)
答:当t取
时△ABP与△QEA全等.
(3)由(1)知△ABP∽△QEA;
∴
=(
)2
∴
=(
)2
整理得:y=
.
 (1)证明:∵四边形ABCD为正方形;
(1)证明:∵四边形ABCD为正方形;∴∠BAP+∠QAE=∠B=90°,
∵QE⊥AP;
∴∠QAE+∠EQA=∠AEQ=90°
∴∠BAP=∠EQA,∠B=∠AEQ;
∴△ABP∽△QEA(AA)
(2)∵△ABP≌△QEA;
∴AP=AQ(全等三角形的对应边相等);
在RT△ABP与RT△QEA中根据勾股定理得AP2=32+t2,AQ2=(2t)2
即32+t2=(2t)2
解得t1=
| 3 |
| 3 |
答:当t取
| 3 |
(3)由(1)知△ABP∽△QEA;
∴
| y |
| S△ABP |
| AQ |
| AP |
∴
| y | ||
|
| 2t | ||
|
整理得:y=
| 3t3 |
| 9+t2 |
看了 如图,正方形ABCD的边长为...的网友还看了以下:
在梯形纸片ABCD中,BC∥AD,∠A+∠D=90度,tanA=2,过点B作BH⊥AD于H,BC=B 2020-03-30 …
正方体ABCD-A’B"C"D"中P,Q,R分别是AB,AD,BC的中点,那么正方体的过P,Q,R 2020-05-13 …
菱形纸片ABCD中,角A=60°,将纸片折叠,点A,D分别落在A' D'处,且A' D'经过B E 2020-05-16 …
将一矩形纸片OABC放在直角坐标系中,O为原点,C在x轴上,OA=6,OC=10.如图,将矩形变为 2020-05-16 …
如图是尿的形成示意图,请据图回答(1)在尿的形成过程中要经过两个作用过程,即图中的A作用和C作用. 2020-06-22 …
如图表示细胞内遗传信息的传递过程,下列有关叙述正确的是()A.图示过程发生在细胞有丝分裂的间期B. 2020-07-21 …
四边形OABC是矩形,OA=4,OC=8,将矩形OABC沿直线Ac折叠四边形OABC是矩形,OA= 2020-07-26 …
读“丹霞地貌形成示意图”,回答下列各题:1.丹霞地貌的形成过程正确的是()A.c→b→d→a→f→e 2020-11-21 …
如图是生态系统中碳循环示意图,图中D为大气,分析回答.(1)碳在大气与A、B、C之间的传递,主要是以 2020-11-22 …
下图表示在人体细胞内发生的一些生化反应()A.а过程除产生丙酮酸外,还有少量ATP和大量[H]生成B 2021-01-22 …