早教吧作业答案频道 -->数学-->
如图1,△ABC和△DEF中,AB=AC,DE=DF,∠A=∠D.(1)求证:BCAB=EFDE;(2)由(1)中的结论可知,等腰三角形ABC中,当顶角∠A的大小确定时,它的对边(
题目详情
如图1,△ABC和△DEF中,AB=AC,DE=DF,∠A=∠D.
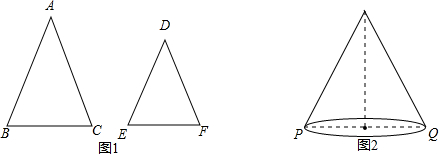
(1)求证:
=
;
(2)由(1)中的结论可知,等腰三角形ABC中,当顶角∠A的大小确定时,它的对边(即底边BC)与邻边(即腰AB或AC)的比值也就确定,我们把这个比值记作T(A),即T(A)=
=
,如T(60°)=1.
①理解巩固:T(90°)=___,T(120°)=___,若α是等腰三角形的顶角,则T(α)的取值范围是___;
②学以致用:如图2,圆锥的母线长为9,底面直径PQ=8,一只蚂蚁从点P沿着圆锥的侧面爬行到点Q,求蚂蚁爬行的最短路径长(精确到0.1).
(参考数据:T(160°)≈1.97,T(80°)≈1.29,T(40°)≈0.68)
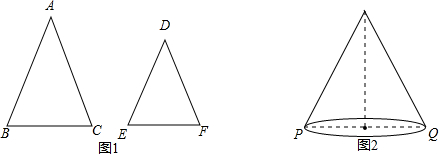
(1)求证:
| BC |
| AB |
| EF |
| DE |
(2)由(1)中的结论可知,等腰三角形ABC中,当顶角∠A的大小确定时,它的对边(即底边BC)与邻边(即腰AB或AC)的比值也就确定,我们把这个比值记作T(A),即T(A)=
| ∠A的对边(底边) |
| ∠A的邻边(腰) |
| BC |
| AB |
①理解巩固:T(90°)=___,T(120°)=___,若α是等腰三角形的顶角,则T(α)的取值范围是___;
②学以致用:如图2,圆锥的母线长为9,底面直径PQ=8,一只蚂蚁从点P沿着圆锥的侧面爬行到点Q,求蚂蚁爬行的最短路径长(精确到0.1).
(参考数据:T(160°)≈1.97,T(80°)≈1.29,T(40°)≈0.68)
▼优质解答
答案和解析
(1)∵AB=AC,DE=DF,
∴
=
,
又∵∠A=∠D,
∴△ABC∽△DEF,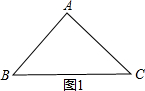
∴
=
;
(2)①如图1,∠A=90°,AB=AC,
则
=
,
∴T(90°)=
,
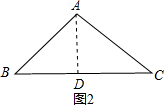 如图2,∠A=90°,AB=AC,
如图2,∠A=90°,AB=AC,
作AD⊥BC于D,
则∠B=60°,
∴BD=
AB,
∴BC=
AB,
∴T(120°)=
;
∵AB-AC<BC<AB+AC,
∴0<T(α)<2,
故答案为:
;
;0<T(α)<2;
②∵圆锥的底面直径PQ=8,
∴圆锥的底面周长为8π,即侧面展开图扇形的弧长为8π,
设扇形的圆心角为n°,
则
=8π,
解得,n=160,
∵T(80°)≈1.29,
∴蚂蚁爬行的最短路径长为1.29×9≈11.6.
∴
| AB |
| DE |
| AC |
| DF |
又∵∠A=∠D,
∴△ABC∽△DEF,

∴
| BC |
| AB |
| EF |
| DE |
(2)①如图1,∠A=90°,AB=AC,
则
| BC |
| AB |
| 2 |
∴T(90°)=
| 2 |
 如图2,∠A=90°,AB=AC,
如图2,∠A=90°,AB=AC,作AD⊥BC于D,
则∠B=60°,
∴BD=
| ||
| 2 |
∴BC=
| 3 |
∴T(120°)=
| 3 |
∵AB-AC<BC<AB+AC,
∴0<T(α)<2,
故答案为:
| 2 |
| 3 |
②∵圆锥的底面直径PQ=8,
∴圆锥的底面周长为8π,即侧面展开图扇形的弧长为8π,
设扇形的圆心角为n°,
则
| n×π×9 |
| 180 |
解得,n=160,
∵T(80°)≈1.29,
∴蚂蚁爬行的最短路径长为1.29×9≈11.6.
看了 如图1,△ABC和△DEF中...的网友还看了以下:
我设置不了悬赏分,你一定会有福报的!1.(1)证明:1\√(n+1)+√n=√(n+1)-√n"\ 2020-05-23 …
已知sn=pn^2+qn+r(其中p,q,r是常数,p不等于0),数列an一定是等差数列吗?如果是 2020-07-20 …
写出下面命题的题设和结论,如果是真命题请在括号内打√,否则打X1.钝角一定大于它的补角.()题设: 2020-07-29 …
(1)利用已知条件和某些数学定义、公理、定理等经过一系列的推理论证最后推导出所要证明的结论成立这种 2020-07-30 …
对的打√,错的打×1.解方程的依据是等式的性质.2.50+2x>72,这是一个方程.3.等式两边同时 2020-11-07 …
请问:倍数问题问题一:6除以2等于3,6是2的倍数。那么,4除以8等于1/2,4是8的1/2倍吗?还 2020-11-15 …
22.请以“你曾陪我一起走过”为题,写一篇不少于700字的记叙文。(40分)要求:1.立意自定2.结 2020-11-30 …
1.已知16^m=4*2^2n-2,27^m=9*3^m+3,求m,n的值.2.下列结论中正确的个数 2020-12-23 …
请以“你曾陪我一起走过”为题,写一篇不少于700字的记叙文。(40分)要求:1.立意自定2.结合生活 2021-01-13 …
总结四边形的定义、判定和性质四边形包括平行四边形、等腰梯形、矩形、菱形、正方形格式:如平行四边形定义 2021-01-22 …