如图，等腰△ABC中，AB=CB，M为ABC内一点，∠MAC+∠MCB=∠MCA=30°（1）求证：△ABM为等腰三角形；（2）求∠BMC的度数．

Question

如图，等腰△ABC中，AB=CB，M为ABC内一点，∠MAC+∠MCB=∠MCA=30°

（1）求证：△ABM为等腰三角形；
（2）求∠BMC的度数．

Answer 1

（1）证明：如图：

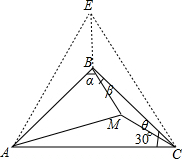
以AC为边作等边三角形ACE，使B、E在AC的同侧，连接BE，
则AE=CE，∠AEC=60°，
设∠MCB=θ，∠ABM=α，∠CBM=β，
在△ABE和△CBE中，

AE=CE

BE=BE

AB=BC

，
∴△ABE≌△CBE（SSS），
∴∠AEB=∠BEC=30°=∠ACM，∠BAE=∠BCE，
∵∠BAE=∠BCE=∠ECA-（∠BCM+∠MCA）=30°-θ=∠MAC，
在△ABE和△AMC中，

∠AEB=∠ACM

AE=AC

∠BAE=∠CAM

，
∴△ABE≌△AMC（ASA），
∴AB=AM，
∴△ABM是等腰三角形；

（2） ∵AB=BC，
∴∠BAC=∠BCA=30°+θ，
∵∠MAC=30°-θ，
∴∠BAM=（30°+θ）-（30°-θ）=2θ，
∵AB=AM，
∴∠ABM=∠AMB=α，
∴α=(1)/(2)（180°-∠BAM）=90°-θ，
∴β=180°-∠BAC-∠BCA-α=30°-θ，
∴∠BMC=180°-β-θ=150°．