如图，已知点A（0，2），B（2，2），C（-1，-2），抛物线F：y=x2-2mx+m2-2与直线x=-2交于点P．（1）当抛物线F经过点C时，求它的表达式；（2）抛物线F上有两点M（x1，y1）、N（x2，y2），若-2≤x1&l

Question

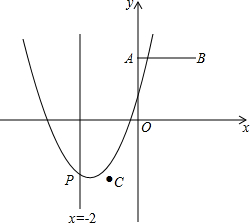
如图，已知点A（0，2），B（2，2），C（-1，-2），抛物线F：y=x²-2mx+m²-2与直线x=-2交于点P．

（1）当抛物线F经过点C时，求它的表达式；
（2）抛物线F上有两点M（x₁，y₁）、N（x₂，y₂），若-2≤x₁<x₂，y₁<y₂，求m的取值范围；
（3）设点P的纵坐标为y_P，求y_P的最小值，此时抛物线F上有两点M（x₁，y₁）、N（x₂，y₂），若x₁<x₂≤-2，比较y₁与y₂的大小；
（4）当抛物线F与线段AB有公共点时，直接写出m的取值范围．

Answer 1

（1）∵抛物线F经过点C（-1，-2），
∴-2=1+2m+m²-2．
∴m=-1．
∴抛物线F的表达式是y=x²+2x-1．
（2）抛物线F的对称轴为：直线x=m，
当x≥m时，y随x的增大而增大；．
点M、N均在直线x=-2的右侧，
∴直线x=-2必须在直线x=m右侧或与之重合．
∴m≤-2．
（3）当x=-2时，yP=4+4m+m2-2=（m+2）²-2．
∴当m=-2时，y_P的最小值=-2．
此时抛物线F的表达式是y=（x+2）²-2．
∴当x≤-2时，y随x的增大而减小．
∵x₁<x₂≤-2，
∴y₁>y₂．
（4）∵y=（x-m）²-2，
∴抛物线的顶点在直线y=-2上．
当x=0时，y=m²-2．
当x=2时，y=m²-4m+2．
∵抛物线与线段AB有交点，
∴（m²-4）（m²-4m）<0，
∴

m2-4>0

m2-4m<0

或

m2-4<0

m2-4m>0

，
解得：-2≤m≤0或2≤m≤4．