早教吧作业答案频道 -->数学-->
已知抛物线y=x2-2mx+4m-8的顶点为A.(1)求证:该抛物线与x轴总有两个交点;(2)当m=1时,直线BC:y=kx-2与该抛物线交于B,C两点,若线段BC被x轴平分,求k的值;(3)以A为一个顶点作该抛物
题目详情
已知抛物线y=x2-2mx+4m-8的顶点为A.
(1)求证:该抛物线与x轴总有两个交点;
(2)当m=1时,直线BC:y=kx-2与该抛物线交于B,C两点,若线段BC被x轴平分,求k的值;
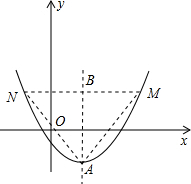
(3)以A为一个顶点作该抛物线的内接正三角形AMN(M,N两点在抛物线上),请问:△AMN的面积是与m无关的定值吗?若是,请求出这个定值;若不是,请说明理由.

(1)求证:该抛物线与x轴总有两个交点;
(2)当m=1时,直线BC:y=kx-2与该抛物线交于B,C两点,若线段BC被x轴平分,求k的值;
(3)以A为一个顶点作该抛物线的内接正三角形AMN(M,N两点在抛物线上),请问:△AMN的面积是与m无关的定值吗?若是,请求出这个定值;若不是,请说明理由.
▼优质解答
答案和解析
 (1)证明:△=4m2-4(4m-8)=4(m-2)2+16>0,则该抛物线与x轴总有两个交点;
(1)证明:△=4m2-4(4m-8)=4(m-2)2+16>0,则该抛物线与x轴总有两个交点;
(2) 当m=1时,y=x2-2x-4.
∵抛物线y=x2-2x-4与直线y=kx-2交于B、C两点,
∴x2-2x-4=kx-2,
整理,得x2-(2+k)x-2=0,
设B(x1,y1),C(x2,y2),则x1+x2=2+k.
∵x轴平分线段PQ,
∴线段BC的中点的纵坐标是0,即
=
=
,
∴
=
,
解得 k=-1±
.
即k的值是:-1±
.
(3) 根据抛物线和正三角形的对称性,可知MN⊥y轴,设抛物线的对称轴与MN交于点B,则AB=
BM.
设M(a,b),
∴BM=a-m(m<a).
又AB=yB-yA=b-(4m-8-m2)=a2-2ma+4m-8-(4m-8-m2)=(a-m)2,
∴(a-m)2=
(a-m),
∴a-m=
,
∴BM=
,AB=3,
∴S△AMN=2×
AB•BM=2×
×3×
=3
 (1)证明:△=4m2-4(4m-8)=4(m-2)2+16>0,则该抛物线与x轴总有两个交点;
(1)证明:△=4m2-4(4m-8)=4(m-2)2+16>0,则该抛物线与x轴总有两个交点;(2) 当m=1时,y=x2-2x-4.
∵抛物线y=x2-2x-4与直线y=kx-2交于B、C两点,
∴x2-2x-4=kx-2,
整理,得x2-(2+k)x-2=0,
设B(x1,y1),C(x2,y2),则x1+x2=2+k.
∵x轴平分线段PQ,
∴线段BC的中点的纵坐标是0,即
| y1+y2 |
| 2 |
| kx1-2+kx2-2 |
| 2 |
| 2+k |
| 2 |
∴
| k(2+k)-4 |
| 2 |
| 2+k |
| 2 |
解得 k=-1±
| 5 |
即k的值是:-1±
| 5 |
(3) 根据抛物线和正三角形的对称性,可知MN⊥y轴,设抛物线的对称轴与MN交于点B,则AB=
| 3 |
设M(a,b),
∴BM=a-m(m<a).
又AB=yB-yA=b-(4m-8-m2)=a2-2ma+4m-8-(4m-8-m2)=(a-m)2,
∴(a-m)2=
| 3 |
∴a-m=
| 3 |
∴BM=
| 3 |
∴S△AMN=2×
| 1 |
| 2 |
| 1 |
| 2 |
| 3 |
作业帮用户
2017-10-14

 |
看了 已知抛物线y=x2-2mx+...的网友还看了以下:
问道数学代数式(一元二次方程)的题由韦达定理得,x1 + x2 = -b/a ,x1 * x2 = 2020-05-13 …
已知坐标原点为0.抛物线X2=4y.直线y=kx+2与抛物线交于A(x1.y1)B(X2.y2)两 2020-05-23 …
占有的不动产或者动产被侵占的,占有人有权请求返还原物,该请求权自侵占发生之日起( )未行使的, 2020-05-27 …
一直线与抛物线x2=y交与a、b两点,他们的横坐标分别为x1、x2,此直线在x轴上的截距为a,求证 2020-06-14 …
(2008•茂名)如图,在平面直角坐标系中,抛物线y=-x2+bx+c经过A(0,-4)、B(x1 2020-07-21 …
知道抛物线的与x轴的两个交点(x1,0),(x2,0),并知道抛物线过某一个点(m,n)设抛物线的 2020-07-24 …
抛物线的数学题,难死了如图,在平面直角坐标系中,抛物线y=负三分之二X的平方+bx+c经过A(0, 2020-07-26 …
已知抛物线x2=2py上点P处的切线方程为x-y-1=0.(1)求抛物线的方程;(2)设A(x1, 2020-07-26 …
(2011•玄武区一模)如图,已知抛物y=-x2+bx+c过点C(3,8),与x轴交于A,B两点, 2020-08-02 …
如图,在平面直角坐标系中,抛物线y=-23x2+bx+c经过A(0,-4)、B(x1,0)C(x2, 2020-11-01 …
 扫描下载二维码
扫描下载二维码