早教吧作业答案频道 -->数学-->
如图:在△ABC中,∠ACB=90°,以BC上一点O为圆心,以OB为半径的圆交AB于点M,交BC于点N.(1)求证:BA•BM=BC•BN;(2)如果CM是O的切线,且M为AB的中点,当BN=4时,求MN的长.
题目详情
如图:在△ABC中,∠ACB=90°,以BC上一点O为圆心,以OB为半径的圆交AB于点M,交BC于点N.
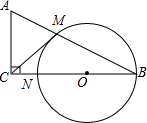
(1)求证:BA•BM=BC•BN;
(2)如果CM是 O的切线,且M为AB的中点,当BN=4时,求MN的长.

(1)求证:BA•BM=BC•BN;
(2)如果CM是 O的切线,且M为AB的中点,当BN=4时,求MN的长.
▼优质解答
答案和解析
(1)证明:如图1,连接MN,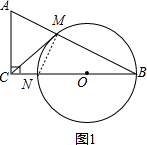
∵NB是 O的直径,
∴∠NMB=90°,
在△ABC和△NBM中,
,
∴△ABC∽△NBM,
∴
=
,
∴BA•BM=BC•BN;
(2)如图2,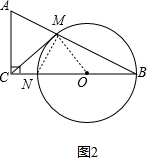 连接MO、MN,
连接MO、MN,
∵∠ACB=90°,M为AB的中点,
∴MC=MB,
∴∠MCB=∠B,
∵CM是 O的切线,
∴∠NMC=∠B,
∵∠MNB=∠NCM+∠NMC,
∴∠MNB=2∠B,
∵BN为 O的直径,
∴∠NMB=90°,
∴∠MNO=60°,
∴△MNO是等边三角形,
∴MN=2.

∵NB是 O的直径,
∴∠NMB=90°,
在△ABC和△NBM中,
|
∴△ABC∽△NBM,
∴
| BA |
| BN |
| BC |
| BM |
∴BA•BM=BC•BN;
(2)如图2,
 连接MO、MN,
连接MO、MN,∵∠ACB=90°,M为AB的中点,
∴MC=MB,
∴∠MCB=∠B,
∵CM是 O的切线,
∴∠NMC=∠B,
∵∠MNB=∠NCM+∠NMC,
∴∠MNB=2∠B,
∵BN为 O的直径,
∴∠NMB=90°,
∴∠MNO=60°,
∴△MNO是等边三角形,
∴MN=2.
看了 如图:在△ABC中,∠ACB...的网友还看了以下:
高二一道求轨迹方程的题~两条直线l,k分别过点A(a,0),B(-a,0)(a为常数),且分别绕A 2020-04-26 …
已知集合A={x┃-1<x<3},集合B={y┃y=1/x,x∈(-3,0)∪(0,1)},集合C 2020-05-15 …
一次函数Y=-MX+N的图形经过第二三四象限,则化简√[M-N]的平方+N的绝对值等于A..B.- 2020-05-16 …
初二数学分式题(全答对追加!)1.若x/y=2,则x²-xy/xy+y²=2.若1/x²-2x+m 2020-05-17 …
数学函数题!2007山东日照)已知二次函数y=x2-x+a(a>0),当自变量x取m时,其相应的函 2020-07-21 …
设向量c=ma+nb(m.n属于R),已知丨a丨=2根号2,丨c丨=4,a垂直于c,b乘c=-4, 2020-07-21 …
若集合A={m|x^2-mx+1=0无实根,m属于R},B={m|mx^2-x+1=0有实根,m属 2020-08-02 …
直线y=2根号下3/3kx+m(-1/2≤k≤1/2)经过A(2根号下3,4)且与y轴交于c,B在y 2020-10-30 …
一道高中数学题,数学高手快来帮忙.若a,b,c∈R,且a的m次方加上b的m次方等于c的m次方,1<m 2020-12-21 …
M是一种治疗艾滋病的新药(结构简式见图),已知M的分子中-NH-COO-基团(除H外)与苯环在同一个 2020-12-22 …