早教吧作业答案频道 -->数学-->
如图,在△ABC中,∠A=∠α,△ABC的内角平分线或外角平分线交于点P,且∠P=∠β.是试求下列各图中∠α与∠β的关系,并选择一个加以证明.图(1)中∠α与∠β的关系是图(2)中∠α与
题目详情
如图,在△ABC中,∠A=∠α,△ABC的内角平分线或外角平分线交于点P,且∠P=∠β.是试求下列各图中∠α与∠β的关系,并选择一个加以证明.
图(1)中∠α与∠β的关系是___
图(2)中∠α与∠β的关系是___
图(3)中∠α与∠β的关系是___
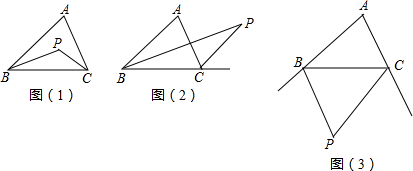
图(1)中∠α与∠β的关系是___
图(2)中∠α与∠β的关系是___
图(3)中∠α与∠β的关系是___

▼优质解答
答案和解析
在图(1)中,根据三角形内角和定理可得:∠ABC+∠ACB=180°-∠A.
∵BP与CP是△ABC的角平分线,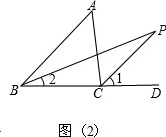
∴∠PBC=
∠ABC,∠PCB=
∠ACB,
∴∠PBC+∠PCB=
(∠ABC+∠ACB)=90°-
α.
在△PBC中,∠BPC=180°-(∠PCB+∠PCB)=180°-(90°-
α)=90°+
α.
∴β=90°+
α.
故答案为:β=90°+
α.
如图(2),结论:∠BPC=
∠A.
证明如下:
∠P=∠1-∠2=
(∠ACD-∠ABC)=
∠A.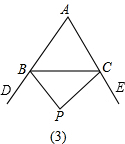
∴β=
α;
故答案为:β=
α;
如图(3)∵BP、CP分别是△ABC两个外角∠CBD和∠BCE的平分线,
∴∠CBP=
(∠A+∠ACB),∠BCP=
(∠A+∠ABC),
∴∠BPC=180°-∠CBP-∠BCP=180°-∠A-
(∠ABC+∠ACB),
∴∠P与∠A的关系是:∠P=180°-∠A-
(∠ABC+∠ACB)=90°-
α,
即β=90°-
α.
故答案为:β=90°-
α.
∵BP与CP是△ABC的角平分线,

∴∠PBC=
| 1 |
| 2 |
| 1 |
| 2 |
∴∠PBC+∠PCB=
| 1 |
| 2 |
| 1 |
| 2 |
在△PBC中,∠BPC=180°-(∠PCB+∠PCB)=180°-(90°-
| 1 |
| 2 |
| 1 |
| 2 |
∴β=90°+
| 1 |
| 2 |
故答案为:β=90°+
| 1 |
| 2 |
如图(2),结论:∠BPC=
| 1 |
| 2 |
证明如下:
∠P=∠1-∠2=
| 1 |
| 2 |
| 1 |
| 2 |

∴β=
| 1 |
| 2 |
故答案为:β=
| 1 |
| 2 |
如图(3)∵BP、CP分别是△ABC两个外角∠CBD和∠BCE的平分线,
∴∠CBP=
| 1 |
| 2 |
| 1 |
| 2 |
∴∠BPC=180°-∠CBP-∠BCP=180°-∠A-
| 1 |
| 2 |
∴∠P与∠A的关系是:∠P=180°-∠A-
| 1 |
| 2 |
| 1 |
| 2 |
即β=90°-
| 1 |
| 2 |
故答案为:β=90°-
| 1 |
| 2 |
看了 如图,在△ABC中,∠A=∠...的网友还看了以下:
下列结论错误的是()A.全等三角形对应边上的高相等B.全等三角形对应边上的中线相等C.两个直角三角 2020-05-20 …
下列说法不正确的是A.三角形的三个内角中,至少有一个钝角B.三角形的三个内角中,至少有一个内角不大 2020-06-26 …
下列说法不正确的是A.三角形的三个内角中,至少有一个钝角B.三角形的三个内角中,至少有一个内角不大 2020-06-26 …
在直角系中0~360°之间,找出与下列各角终边相同的角,并判断它们各是哪个象限的角,(1)-在直角 2020-07-09 …
证明下列真命题的逆命题是假命题1如果两个角都是直角,那么这两个角相等2如果三角形中有一个角是钝角, 2020-07-21 …
下列定理中,没有逆定理的是()A.内错角相等,两直线平行下列定理中,没有逆定理的是()A.内错角相 2020-07-23 …
下列说法中,错误的有①一个角的平分线是一条射线;②三角形中的角平分线是下列说法中,错误的有①一个角 2020-07-30 …
用反证法证明“一个三角形中至少有两个锐角”时,下列假设正确的是()A.假设一个三角形中只有一个锐角 2020-08-01 …
下列诸多条件中,不能确定是直角三角形的是……………(下列诸多条件中,不能确定是直角三角形的是………… 2020-12-14 …
图中的三角形称为希尔宾斯三角形,在下列四个三角形中,黑色三角形的个数依次构成数列{an}的前四项,依 2020-12-25 …