早教吧作业答案频道 -->数学-->
问题提出把多边形的任一边向两方延长,如果其它各边都在延长线的同一旁,则这样的多边形为凸多边形.如平行四边形、梯形等都是凸多边形.我们教材中所说的多边形如没作特别说明,
题目详情
问题提出
把多边形的任一边向两方延长,如果其它各边都在延长线的同一旁,则这样的多边形为凸多边形.如平行四边形、梯形等都是凸多边形.我们教材中所说的多边形如没作特别说明,一般都是指凸多边形.
把多边形的某些边向两方延长,其他各边有不在延长所得直线的同一旁,这样的多边形叫做凹多边形.凹多边形会有哪些性质呢?
初步认识
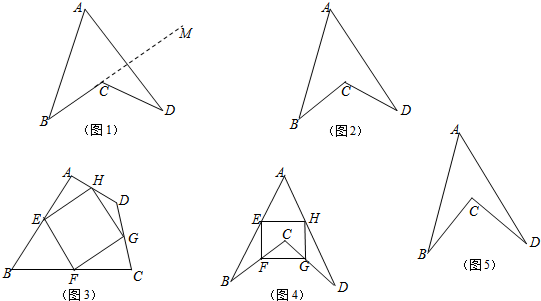
如图(1),四边形ABCD中,延长BC到M,则边AB、CD分别在直线BM的两旁,所以四边形ABCD就是一个凹四边形.请你画一个凹五边形.(不要说明)
性质探究
请你完成凹四边形一个性质的证明:
如图(2),在凹四边形ABCD中,求证:∠BCD=∠A+∠B+∠D.
类比学习
我们以前曾研究过凸四边形的中点四边形问题,如图(3),在四边形ABCD中,E、F、G、H分别是边AB、BC、CD、DA的中点,则四边形EFGH是平行四边形.当四边形ABCD满足一定条件时,四边形EFGH还可能是矩形、菱形或正方形.
如图(4),在凹四边形ABCD中,AB=AD,CB=CD,E、F、G、H分别是边AB、BC、CD、DA的中点,请判断四边形EFGH的形状,并证明你的结论.
拓展延伸
如图(5),在凹四边形ABCD的边上求作一点P,使得∠BPD=∠A+∠B+∠D.(不写作法、证明,保留作图痕迹)
把多边形的任一边向两方延长,如果其它各边都在延长线的同一旁,则这样的多边形为凸多边形.如平行四边形、梯形等都是凸多边形.我们教材中所说的多边形如没作特别说明,一般都是指凸多边形.
把多边形的某些边向两方延长,其他各边有不在延长所得直线的同一旁,这样的多边形叫做凹多边形.凹多边形会有哪些性质呢?
初步认识
如图(1),四边形ABCD中,延长BC到M,则边AB、CD分别在直线BM的两旁,所以四边形ABCD就是一个凹四边形.请你画一个凹五边形.(不要说明)
性质探究
请你完成凹四边形一个性质的证明:
如图(2),在凹四边形ABCD中,求证:∠BCD=∠A+∠B+∠D.
类比学习
我们以前曾研究过凸四边形的中点四边形问题,如图(3),在四边形ABCD中,E、F、G、H分别是边AB、BC、CD、DA的中点,则四边形EFGH是平行四边形.当四边形ABCD满足一定条件时,四边形EFGH还可能是矩形、菱形或正方形.
如图(4),在凹四边形ABCD中,AB=AD,CB=CD,E、F、G、H分别是边AB、BC、CD、DA的中点,请判断四边形EFGH的形状,并证明你的结论.
拓展延伸
如图(5),在凹四边形ABCD的边上求作一点P,使得∠BPD=∠A+∠B+∠D.(不写作法、证明,保留作图痕迹)

▼优质解答
答案和解析
初步认识:如图1,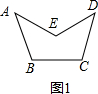 ;
;
性质探究:
延长BC交AD于点M,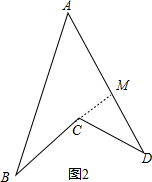
∵∠BCD是△CDE的外角,
∴∠BCD=∠CMD+∠D,
同理,∠CED是△ABE的外角,
∴∠CMD=∠A+∠B,
∴∠BCD=∠A+∠B+∠D;
类比学习: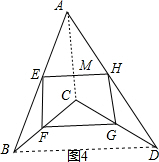
四边形EFGH是矩形,
证明:连接AC,BD,交EH于点M,
∵E、F、G、H分别是边AB、BC、CD、DA的中点,
∴EF=HG=
AC,EF∥HG∥AC,
∴四边形EFGH是平行四边形,
∵AB=AD,BC=DC,
∴A、C在BD的垂直平分线上,
∴AM⊥EH,
已证EF∥AC,同理可证FG∥BD,
∴∠EFG=90°,
∴□EFGH是矩形;
拓展延伸:
如图所示,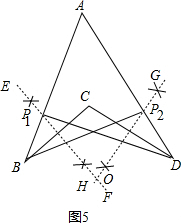 .
.
 ;
;性质探究:
延长BC交AD于点M,

∵∠BCD是△CDE的外角,
∴∠BCD=∠CMD+∠D,
同理,∠CED是△ABE的外角,
∴∠CMD=∠A+∠B,
∴∠BCD=∠A+∠B+∠D;
类比学习:

四边形EFGH是矩形,
证明:连接AC,BD,交EH于点M,
∵E、F、G、H分别是边AB、BC、CD、DA的中点,
∴EF=HG=
| 1 |
| 2 |
∴四边形EFGH是平行四边形,
∵AB=AD,BC=DC,
∴A、C在BD的垂直平分线上,
∴AM⊥EH,
已证EF∥AC,同理可证FG∥BD,
∴∠EFG=90°,
∴□EFGH是矩形;
拓展延伸:
如图所示,
 .
.
看了 问题提出把多边形的任一边向两...的网友还看了以下:
两直线3x+y-3=0与6x+2y+1=0平行,则它们之间的距离为就想知道是怎么算出来的最后一步就 2020-05-13 …
若两图形关于某条直线对称,且它们的对应线段相交,则交点必在 上,若对应线段互相平行,则它们必都与 2020-05-15 …
在河的A到B段水流速度很慢,几乎不动,不妨看做静水.而从B到C段却流的很快,船从A到C需要3小时, 2020-05-16 …
在河的A到B段水流速度很慢,几乎不动,不妨看做静水.而从B到C段却流的很快,船从A到C需要3小时, 2020-05-16 …
选择真命题:A.如果两个不重合的平面有两个不同的公共点A,B,那么这两个平面有无数个公共点并且这些 2020-06-06 …
地面上一块砖宽AB=2cm,长BC=10cm,CD上的点G距地面高CG=5cm,地面上一只蚂蚁从A 2020-07-11 …
两条直线平行,则它们是否共面?为什么? 2020-07-25 …
给出下列几个命题:①若某平面的两条斜线段相等则它们在此平面上的射影相等;②若两条斜线段在平面上的射 2020-07-30 …
一艘飞艇在无风时,航速是(根号3)akm/h,在某时刻正刮北风,风速akm/h飞艇向正东方向航行,则 2020-12-23 …
定义满足下列两个条件的矩阵称为阶梯形矩阵:\x05(1)如果该矩阵有零行,则它们位于矩阵的最下方;\ 2020-12-24 …