早教吧作业答案频道 -->数学-->
已知凸四边形ABCD中,∠A=∠C=90°.(1)如图1,若DE平分∠ADC,BF平分∠ABC的邻补角,判断DE与BF位置关系并证明;(2)如图2,若BF、DE分别平分∠ABC、∠ADC的邻补角,判断DE与BF位置关系并证
题目详情
已知凸四边形ABCD中,∠A=∠C=90°.
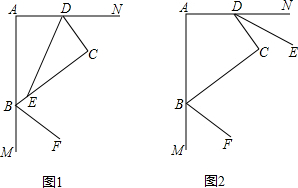
(1)如图1,若DE平分∠ADC,BF平分∠ABC的邻补角,判断DE与BF位置关系并证明;
(2)如图2,若BF、DE分别平分∠ABC、∠ADC的邻补角,判断DE与BF位置关系并证明.
(1)如图1,若DE平分∠ADC,BF平分∠ABC的邻补角,判断DE与BF位置关系并证明;
(2)如图2,若BF、DE分别平分∠ABC、∠ADC的邻补角,判断DE与BF位置关系并证明.

▼优质解答
答案和解析
(1)DE⊥BF,
延长DE交BF于点G
∵∠A+∠ABC+∠C+∠ADC=360°
又∵∠A=∠C=90°,
∴∠ABC+∠ADC=180°
∵∠ABC+∠MBC=180°
∴∠ADC=∠MBC,
∵DE、BF分别平分∠ADC、∠MBC
∴∠EDC=
∠ADC,∠EBG=
∠MBC,
∴∠EDC=∠EBG,
∵∠EDC+∠DEC+∠C=180°
∠EBG+∠BEG+∠EGB=180°
又∵∠DEC=∠BEG∴∠EGB=∠C=90
∴DE⊥BF;
(2)DE∥BF,
连接BD,
∵DE、BF分别平分∠NDC、∠MBC
∴∠EDC=
∠NDC,∠FBC=
∠MBC,
∵∠ADC+∠NDC=180°
又∵∠ADC=∠MBC
∴∠MBC+∠NDC=180°
∴∠EDC+∠FBC=90°,
∵∠C=90°∴∠CDB+∠CBD=90°
∴∠EDC+∠CDB+∠FBC+∠CBD=180°
即∠EDB+∠FBD=180°,
∴DE∥BF.
延长DE交BF于点G
∵∠A+∠ABC+∠C+∠ADC=360°
又∵∠A=∠C=90°,
∴∠ABC+∠ADC=180°
∵∠ABC+∠MBC=180°
∴∠ADC=∠MBC,
∵DE、BF分别平分∠ADC、∠MBC
∴∠EDC=
| 1 |
| 2 |
| 1 |
| 2 |
∴∠EDC=∠EBG,
∵∠EDC+∠DEC+∠C=180°
∠EBG+∠BEG+∠EGB=180°
又∵∠DEC=∠BEG∴∠EGB=∠C=90
∴DE⊥BF;
(2)DE∥BF,
连接BD,
∵DE、BF分别平分∠NDC、∠MBC
∴∠EDC=
| 1 |
| 2 |
| 1 |
| 2 |
∵∠ADC+∠NDC=180°
又∵∠ADC=∠MBC
∴∠MBC+∠NDC=180°
∴∠EDC+∠FBC=90°,
∵∠C=90°∴∠CDB+∠CBD=90°
∴∠EDC+∠CDB+∠FBC+∠CBD=180°
即∠EDB+∠FBD=180°,
∴DE∥BF.
看了 已知凸四边形ABCD中,∠A...的网友还看了以下:
谁来帮我做到高三数学题被,如图所示,已知平面α‖平面β‖平面γ,且β位于α与γ之间,点A,D属于平 2020-05-13 …
中国政府一贯致力于和平、发展、合作,奉行与邻为善、以邻为伴周边外交方针和安邻、睦邻、友邻、富邻政策 2020-06-18 …
平角与邻补角的区别是什么? 2020-06-18 …
《左传•隐公六年》“亲仁善邻,国之宝也。”对这一贵和思想理解正确的是()①这是国与国,家与家,人与 2020-07-16 …
读东北地区图,写出图中字母代表的地理事物名称:(1)省级行政区名称:A,B,C,D.(2)地形区: 2020-07-25 …
《左传·隐公六年》“亲仁善邻,国之宝也。”对这一贵和思想理解正确的是[]①这是国与国,家与家,人与 2020-07-25 …
有A、B、C、D、E、F六人围一张圆桌而坐,已知E与C相隔一人并坐在C的右面(如图),D坐在A的对面 2020-11-28 …
中国政府一贯致力于和平、发展、合作,奉行“与邻为善、以邻为伴”的周边外交方针,高度重视发展与周边国家 2020-11-30 …
温家宝总理在首届东亚峰会上提出:“中国将走和平发展道路,将继续坚定地奉行与邻为善、以邻为伴的方针和睦 2021-01-13 …
中国政府致力于和平、发展、合作,奉行与邻为善、以邻为伴的周边外交方针和安邻、富邻的政策,高度重视加强 2021-01-13 …