早教吧作业答案频道 -->数学-->
已知∠ABC=∠DBE,射线BD在∠ABC的内部,按要求完成下列各小题.尝试探究:如图1,已知∠ABC=90°,当BD是∠ABC的平分线时,∠ABE+∠DBC的度数为;初步应用:如图2,已知∠ABC=90°,若BD
题目详情
已知∠ABC=∠DBE,射线BD在∠ABC的内部,按要求完成下列各小题.
尝试探究:如图1,已知∠ABC=90°,当BD是∠ABC的平分线时,∠ABE+∠DBC的度数为___;
初步应用:如图2,已知∠ABC=90°,若BD不是∠ABC的平分线,求∠ABE+∠DBC的度数;
拓展提升:如图3,若∠ABC=45°时,试判断∠ABE与∠DBC之间的数量关系,并说明理由.
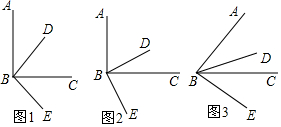
尝试探究:如图1,已知∠ABC=90°,当BD是∠ABC的平分线时,∠ABE+∠DBC的度数为___;
初步应用:如图2,已知∠ABC=90°,若BD不是∠ABC的平分线,求∠ABE+∠DBC的度数;
拓展提升:如图3,若∠ABC=45°时,试判断∠ABE与∠DBC之间的数量关系,并说明理由.

▼优质解答
答案和解析
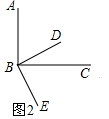 尝试探究:∵∠ABC=90°,BD平分∠ABC,
尝试探究:∵∠ABC=90°,BD平分∠ABC,
所以∠DBC=45°,
因为∠DBE=∠ABC=90°,∠DBC+∠CBE=∠DBE
所以∠CBE=45°.
所以∠ABE+∠DBC=∠ABC+∠CBE+∠DBC=90°+45°+45°=180°.
初步应用:因为∠DBE=∠ABC=90°,
所以∠ABE+∠DBC=∠ABC+∠CBE+∠DBC
=∠ABC+∠DBE=180°.
答:∠ABE+∠DBC的度数为180°.
拓展提升:∠ABE+∠DBC=90°.
理由: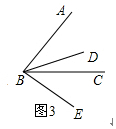
因为∠DBE=∠ABC=45°,
所以∠ABE+∠DBC=∠ABC+∠CBE+∠DBC
=∠ABC+∠DBE=90°.
 尝试探究:∵∠ABC=90°,BD平分∠ABC,
尝试探究:∵∠ABC=90°,BD平分∠ABC,所以∠DBC=45°,
因为∠DBE=∠ABC=90°,∠DBC+∠CBE=∠DBE
所以∠CBE=45°.
所以∠ABE+∠DBC=∠ABC+∠CBE+∠DBC=90°+45°+45°=180°.
初步应用:因为∠DBE=∠ABC=90°,

所以∠ABE+∠DBC=∠ABC+∠CBE+∠DBC
=∠ABC+∠DBE=180°.
答:∠ABE+∠DBC的度数为180°.
拓展提升:∠ABE+∠DBC=90°.
理由:

因为∠DBE=∠ABC=45°,
所以∠ABE+∠DBC=∠ABC+∠CBE+∠DBC
=∠ABC+∠DBE=90°.
看了 已知∠ABC=∠DBE,射线...的网友还看了以下:
如图是关于人体免疫的图解,属于保卫人体的第一道防线的图是:()A.A图和B图B.A图C.B图和D图 2020-05-02 …
A、B两图分别表示玉米种子和菜芽种子的结构,请据图回答问题(注:[]内填图中代码,横线上填相应的名 2020-05-13 …
A、B两图分别表示玉米种子和菜芽种子的结构,请据图回答问题(注:[]内填图中代码,横线上填相应的名 2020-05-13 …
如图表示细胞周期,下列叙述错误的是()A.a→b为分裂期B.b→a为分裂间期C.a→b→a表示一个 2020-05-14 …
CAD技术中用x、y方向的像素点来表示的分辨率是______。A.图形输入分辨率B.绘图分辨率C. 2020-05-23 …
CAD技术中用x、y方向的像素点来表示的分辨率是()。A.图形输入分辨率B.绘图分辨率C.捕捉分辨率 2020-05-24 …
A、B两图分别表示某种高等动物正在进行减数分裂的细胞,据图回答:(1)A图表示分裂的期,该细胞分裂 2020-06-10 …
A、B两图分别为两个草原生态系统的食物网示意图,请据图回答下列问题:(1)比较图A与图B所示食物网 2020-06-22 …
(x+y):x=10:7,x:y=(p-q):p=2:3,p:q=a:b=3:5,a:(b-a)= 2020-08-03 …
若全球气候持续变暖,则可能出现的现象是()A.a图等温线变得更加密集B.a图0℃等温线向北移动C.b 2020-11-02 …