早教吧作业答案频道 -->数学-->
如图,正方形ABCD中,点P是射线BC上的任意一点(点B与点C除外),连接DP,分别过点C,A作直线DP的垂线,垂足为点E,F.(1)当点P在BC的延长线上时,那么线段AF、CE、EF之间有怎样的数量关
题目详情
如图,正方形ABCD中,点P是射线BC上的任意一点(点B与点C除外),连接DP,分别过点C,A作直线DP的垂线,垂足为点E,F.
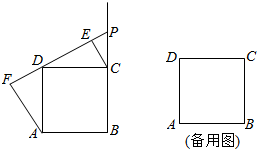
(1)当点P在BC的延长线上时,那么线段AF、CE、EF之间有怎样的数量关系?请证明你的结论;
(2)当点P在边BC上时,联结AP,正方形的边长为2,设CE=x,AF=y.求y与x的函数解析式.并写出函数的定义域;
(3)在(2)的条件下,当x=1时.求EF的长.

(1)当点P在BC的延长线上时,那么线段AF、CE、EF之间有怎样的数量关系?请证明你的结论;
(2)当点P在边BC上时,联结AP,正方形的边长为2,设CE=x,AF=y.求y与x的函数解析式.并写出函数的定义域;
(3)在(2)的条件下,当x=1时.求EF的长.
▼优质解答
答案和解析
(1)AF+CE=EF.证明如下:
∵AD=DC,∠AFD=∠DEC,∠ADF=∠DCE,∴△ADF≌△DCE,∴DF=CE,AF=DE,∴AF+CE=EF.
(2)由(1)的证明,可知DF=CE,AF=DE.由CE=x,AF=y,得DE=y.
于是,在Rt△CDE中,CD=2,利用勾股定理,得CE2+DE2=CD2,即得x2+y^2=4.
∴y=
,
∴所求函数解析式为y=
,函数定义域为(0,
);.
(3)当x=1时,得y=
.即得DE=
又∵DF=CE=1,EF=DE-DF,∴EF=
-1
∵AD=DC,∠AFD=∠DEC,∠ADF=∠DCE,∴△ADF≌△DCE,∴DF=CE,AF=DE,∴AF+CE=EF.
(2)由(1)的证明,可知DF=CE,AF=DE.由CE=x,AF=y,得DE=y.
于是,在Rt△CDE中,CD=2,利用勾股定理,得CE2+DE2=CD2,即得x2+y^2=4.
∴y=
| 4-x2 |
∴所求函数解析式为y=
| 4-x2 |
| 2 |
(3)当x=1时,得y=
| 3 |
| 3 |
又∵DF=CE=1,EF=DE-DF,∴EF=
| 3 |
看了 如图,正方形ABCD中,点P...的网友还看了以下:
下列有关晨昏线的说法,正确的是().A.晨昏圈就是经线圈B.晨昏圈与纬线平行C.若晨昏圈与经线圈重 2020-05-23 …
关于经线和纬线的叙述正确的是A经线和纬线一样长B所有经线都与本初字午线平行C纬度越低纬线越长D纬线 2020-06-04 …
求救已知线段AB=20cm,点M是线段AB的中点,点C是线段AB的延长线上的点,AC=3BC,点D 2020-06-06 …
电气间隙是指两个裸露导体之间的()空间距离。A.最短B.平均C.最长D.直线 2020-06-07 …
1.如图所示,已知线段AB=20cm,点M是线段AB中点,点C是线段AB延长线上的点,AC=3BC 2020-07-25 …
一个半径为10厘米,中心角为135度的扇形,D点、E点是弧BC的三等分点,那么阴影部分的面积为多少 2020-08-01 …
如图,在三角形ABC中,AB=AC=5,BC=6,AH垂直于BC于H,D为线段CH上一点,过点D作 2020-08-02 …
如图是小明同学在体育课上跳远后留下的脚印,则表示他的跳远成绩是()A.线段AC的长B.线段BC的长C 2020-10-30 …
读南美洲国家厄瓜多尔地图,下列说法正确的是()A.图中A地坐标是(0°,80°E)B.厄瓜多尔主要位 2020-11-12 …
关于无线电波的传播方式,下列说法正确的是()A.地波的波长较长,能够沿着地表空间传播B.天波的波长较 2020-12-08 …