早教吧作业答案频道 -->数学-->
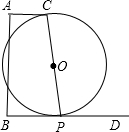
如图,CA⊥AB,DB⊥AB,已知AC=4,AB=10,点P射线BD上一动点,以CP为直径作O,点P运动时.若O与线段AB有公共点,则BP最大值为.
题目详情
如图,CA⊥AB,DB⊥AB,已知AC=4,AB=10,点P射线BD上一动点,以CP为直径作 O,点P运动时.若 O与线段AB有公共点,则BP最大值为___.

▼优质解答
答案和解析
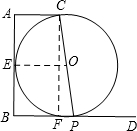 当AB与 O相切时,PB的值最大,如图,
当AB与 O相切时,PB的值最大,如图,
设AB与 O相切于点E,连接OE,则OE⊥AB,
过C作CF⊥PB于F,
∵CA⊥AB,BD⊥AB,
∴AC∥OE∥PB,
∴四边形ABFC是矩形,
∴CF=AB=10,
∵CO=OP,
∴AE=BE,
∴OE是梯形ABPC的中位线,
∴OE=
(AC+PB),
设PB=x,则OE=
(4+x),
∴PC=2OE=4+x,PF=x-4,
由勾股定理得:102+(x-4)2=(4+x)2,
解得:x=
,
∴BP最大值为
;
故答案为:
.
 当AB与 O相切时,PB的值最大,如图,
当AB与 O相切时,PB的值最大,如图,设AB与 O相切于点E,连接OE,则OE⊥AB,
过C作CF⊥PB于F,
∵CA⊥AB,BD⊥AB,
∴AC∥OE∥PB,
∴四边形ABFC是矩形,
∴CF=AB=10,
∵CO=OP,
∴AE=BE,
∴OE是梯形ABPC的中位线,
∴OE=
| 1 |
| 2 |
设PB=x,则OE=
| 1 |
| 2 |
∴PC=2OE=4+x,PF=x-4,
由勾股定理得:102+(x-4)2=(4+x)2,
解得:x=
| 25 |
| 4 |
∴BP最大值为
| 25 |
| 4 |
故答案为:
| 25 |
| 4 |
看了 如图,CA⊥AB,DB⊥AB...的网友还看了以下:
向量共面的必要条件是什么?(或解释向量p=xa+yb中,为什么ab共线,p与ab共面不成立?)—— 2020-05-13 …
如图所示,A船从港口P出发去拦截正以速度v0沿直线航行的B船,A船启动时,B船位于M位置,P与B船 2020-06-23 …
关于公式p=Fv说法正确的是()A.p与F成正比B.p与v成正比C.F与v成反比D.p一定时,F与v 2020-10-30 …
以下关于P、Q、M、N四点取值的判断,正确的是()A、P与M的值相等,且可能小于66°34′B、N为 2020-11-03 …
△ABC,BP,CP分别是∠ABC,∠ACB的平分线,∠P与∠A满足数量关系:∠P=90°+二分之一 2020-11-19 …
△ABC,BP,CP分别是∠ABC,∠ACB的平分线,∠P与∠A满足数量关系:∠P=90°+二分之一 2020-11-19 …
5个选手P,Q,R,S,T举行一场赛跑.P胜Q,P胜R,Q胜S,并且T在P之后,Q之前跑完全程.谁不 2021-01-01 …
5个选手P、Q、R、S、T举行一场赛跑,P胜Q,Q胜R,并且T在P之后,Q之前跑完全程,谁不可能得第 2021-01-01 …
5个选手P,Q,R,S,T举行一场赛跑.P胜Q,P胜R,Q胜S,并且T在P之后,Q之前跑完全程.谁不 2021-01-01 …
如图为某地正午太阳高度角的年变化示意图,读图回答22-23题.以下关于P、Q、M、N四点取值的判断, 2021-01-23 …