已知点A（0，2），B（-1，0），C（2，0），P为线段AO上一动点．（1）求AP+2BP的最小值及点P的坐标；（2）求AP+5CP的最小值及点P的坐标．

Question

已知点A（0，2），B（-1，0），C（2，0），P为线段AO上一动点．
（1）求AP+√(2)BP的最小值及点P的坐标；
（2）求AP+√(5)CP的最小值及点P的坐标．

Answer 1

（1）如图1中，将线段BP绕点B顺时针旋转90得到相等BE，作EM⊥y轴于M，BF⊥ME于F．

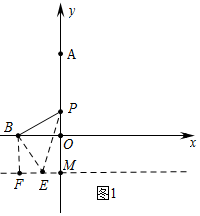
∵∠BFM=∠FMO=∠BOM=90°，
∴四边形OBFM是矩形，
∴∠OBF=∠PBE=90°，
∴∠PBO=∠FBE，
在△BOP和△BFE中，

∠PBO=∠FBE

∠BOP=∠BFE

BP=BE

，
∴△BOP≌△BFE，
∴OB=BF=OM=1，
∴点P在运动时，点E在直线y=-1时运动，
∵PE=√(2)PB，
∴PA+√(2)PB=AP+PE，
∴欲求PA+√(2)PB的最小值，就是求AP+PE的最小值，
∴当点E与点M重合时，根据垂线段最短，可知AP+PE的最小值=AM=OA+OM=3，
∴AP+√(2)BP的最小值为3，此时点P的坐标为（0，1）．

（2）如图2中，作CE⊥PC，使得CE=2PC，连接PE，则PE=√(5)PC．作EF⊥x轴于F．

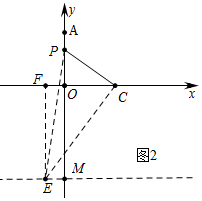
∵∠PCO+∠ECF=90°，∠ECF+∠FEC=90°，
∴∠PCO=∠FEC，∵∠POC=∠EFC=90°，
∴△POC∽△CFE，
∴(OC)/(EF)=(PC)/(EC)=(1)/(2)，∵OC=2，
∴EF=OM=4，
∴点P运动时，点E在直线y=-4上运动，
∴AP+√(5)PC=AP+PE，
∴当E与M重合时，AP+√(5)PC最小值为线段AM的长，
∴AP+

作业帮用户 2017-09-27

扫描下载二维码

©2019 作业帮 联系方式：[e-mail]  作业帮协议