早教吧作业答案频道 -->数学-->
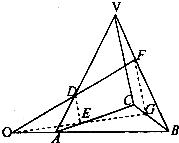
在三棱锥V-ABC中,D、E、F分别是VA、VB、VC上的点并且ADAV=AEAC=VFVB=CGCB=13.求证:直线DF、EG、AB共点.
题目详情
在三棱锥V-ABC中,D、E、F分别是VA、VB、VC上的点并且
=
=
=
=
.求证:直线DF、EG、AB共点.
| AD |
| AV |
| AE |
| AC |
| VF |
| VB |
| CG |
| CB |
| 1 |
| 3 |

▼优质解答
答案和解析
证明:∵
=
=
=
=
,
∴DE∥VC,FG∥VC,DE=
VC,FG=
VC,
∴DE∥FG,DE=
FG,
∴直线DF、EG交于一点O,
∴O∈DF,O∈EG,
∴O∈平面VAG,O∈平面VAB,
∵平面VAG∩平面VAB=AB,
∴O∈AB,
∴直线DF、EG、AB共点O.
| AD |
| AV |
| AE |
| AC |
| VF |
| VB |
| CG |
| CB |
| 1 |
| 3 |
∴DE∥VC,FG∥VC,DE=
| 1 |
| 3 |
| 2 |
| 3 |
∴DE∥FG,DE=
| 1 |
| 2 |
∴直线DF、EG交于一点O,
∴O∈DF,O∈EG,
∴O∈平面VAG,O∈平面VAB,
∵平面VAG∩平面VAB=AB,
∴O∈AB,
∴直线DF、EG、AB共点O.
看了 在三棱锥V-ABC中,D、E...的网友还看了以下:
(1)把图中的长方形按1:2的比例在网格线上画出来.(2)把图中的梯形按2:1的比例在网格线上画出 2020-04-09 …
八年级(3)班两位同学在打羽毛球,一不小心球落在离地面高为6米的树上.其中一位同学赶快搬来一架长为 2020-05-13 …
小明背着书包欢快地走在通往学校的路上.问:小明背上的书包是运动的,还是静止的?说明你判断的依据. 2020-05-13 …
八年级(3)班两位同学在打羽毛球,一不小心球落在离地面高为6米的树上.其中一位同学赶快搬来一架长为 2020-06-10 …
八年级(3)班两位同学在打羽毛球,一不小心球落在离地面高为6米的树上.其中一位同学赶快搬来一架长为 2020-06-10 …
八年级(3)班两位同学在打羽毛球,一不小心球落在离地面高为6米的树上.其中一位同学赶快搬来一架长为 2020-06-10 …
学习了光学知识后,爱动脑筋的小桐和小朵想自己探究小孔成像现象.如图所示,她们给两个空罐的底部中央分 2020-06-10 …
一均匀杆长L=5m,物重G=100N.杆的A端搁在地面上不动,B端放在一人的肩上.如果人的肩高H= 2020-06-27 …
比一比,看看下图中的辣椒、玉米、黄瓜和苹果谁轻谁重.给最轻的打上“○”,最重的打上“√”. 2020-06-27 …
如图,在四边形ABCD中,∠D=90°,AC平分∠DAB,且点C在以AB为直径的⊙O上.(1)求证 2020-07-09 …