早教吧作业答案频道 -->数学-->
如图,在△ABC中,AB=AC,点D在△ABC内,BD=BC,∠DBC=60°,点E在△ABC外,∠BCE=150°,∠ABE=60°.(1)求∠ADB的度数;(2)判断△ABE的形状并加以证明;(3)连接DE,若DE⊥BD,DE=8,求AD的长.
题目详情
如图,在△ABC中,AB=AC,点D在△ABC内,BD=BC,∠DBC=60°,点E在△ABC外,∠BCE=150°,∠ABE=60°.
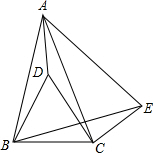
(1)求∠ADB的度数;
(2)判断△ABE的形状并加以证明;
(3)连接DE,若DE⊥BD,DE=8,求AD的长.

(1)求∠ADB的度数;
(2)判断△ABE的形状并加以证明;
(3)连接DE,若DE⊥BD,DE=8,求AD的长.
▼优质解答
答案和解析
(1) ∵BD=BC,∠DBC=60°,
∴△DBC是等边三角形,
∴DB=DC,∠BDC=∠DBC=∠DCB=60°,
在△ADB和△ADC中,
,
∴△ADB≌△ADC,
∴∠ADB=∠ADC,
∴∠ADB=
(360°-60°)=150°.
(2) 结论:△ABE是等边三角形.
理由:∵∠ABE=∠DBC=60°,
∴∠ABD=∠CBE,
在△ABD和△EBC中,
,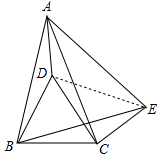
∴△ABD≌△EBC,
∴AB=BE,∵∠ABE=60°,
∴△ABE是等边三角形.
(3) 连接DE.
∵∠BCE=150°,∠DCB=60°,
∴∠DCE=90°,
∵∠EDB=90°,∠BDC=60°,
∴∠EDC=30°,
∴EC=
DE=4,
∵△ABD≌△EBC,
∴AD=EC=4.
∴△DBC是等边三角形,
∴DB=DC,∠BDC=∠DBC=∠DCB=60°,
在△ADB和△ADC中,
|
∴△ADB≌△ADC,
∴∠ADB=∠ADC,
∴∠ADB=
| 1 |
| 2 |
(2) 结论:△ABE是等边三角形.
理由:∵∠ABE=∠DBC=60°,
∴∠ABD=∠CBE,
在△ABD和△EBC中,
|

∴△ABD≌△EBC,
∴AB=BE,∵∠ABE=60°,
∴△ABE是等边三角形.
(3) 连接DE.
∵∠BCE=150°,∠DCB=60°,
∴∠DCE=90°,
∵∠EDB=90°,∠BDC=60°,
∴∠EDC=30°,
∴EC=
| 1 |
| 2 |
∵△ABD≌△EBC,
∴AD=EC=4.
看了 如图,在△ABC中,AB=A...的网友还看了以下:
如图1,MN∥EF,C为两直线之间一点.(1)如图1,若∠MAC与∠EBC的平分线相交于点D,若∠ 2020-06-11 …
如图,直线AB,CD分别与直线AC相交于点A,C,与直线BD相交于点B,D.若∠1=∠2,∠3=7 2020-06-18 …
如图,已知P为△ABC内一点,BP的延长线交AC于点D,若∠1=(9m-5)°,∠2=(8m+6) 2020-07-12 …
(2014•黄浦区一模)已知函数f(x)=ax2+bx+cx+d(其中a,b,c,d是实数常数,x 2020-07-14 …
已知⊙O的半径r=3,设圆心O到一条直线的距离为d,圆上到这条直线的距离为2的点的个数为m,给出下 2020-07-14 …
设数列xn与yn满足xn*yn→0(当n→+∞),则下列断言正确的是()(A)若xn发散,则yn必 2020-07-31 …
下列说法中,正确的是()A.若∠1+∠2+∠3=180°,则∠1、∠2、∠3互为补角B.若∠1是∠ 2020-08-02 …
在A+B=C+D中,若1、6克A和B的混合物完全反应,生成C和D的质量比为3:5,则D为多少克 2020-10-31 …
(2011•淄博)如图,直线AB,CD分别与直线AC相交于点A,C,与直线BD相交于点B,D.若∠1 2020-11-13 …
判断下列命题的真假已知a,b,c,d∈R(1)若ac>bc,则a>b(2)若a>-b,则c-ab>c 2020-12-13 …