早教吧作业答案频道 -->数学-->
已知二次函数y1=-x2-2mx-m2-1(m是常数).(1)求证:不论m为何值,该函数的图象与x轴没有公共点;(2)当m=1时,将函数y1=-x2-2mx-m2-1的图象向上平移5个单位,得到函数y2=-x2+bx+c的图象,且y2=-x
题目详情
已知二次函数y1=-x2-2mx-m2-1(m是常数).
(1)求证:不论m为何值,该函数的图象与x轴没有公共点;
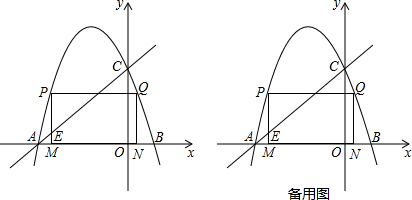
(2)当m=1时,将函数y1=-x2-2mx-m2-1的图象向上平移5个单位,得到函数y2=-x2+bx+c的图象,且y2=-x2+bx+c的图象与x轴交于A、B两点(点A在点B的左边),与y轴交于点C,如图所示.
①求点A、B、C的坐标;
②如图,矩形MPQN的顶点M、N在线段AB上(点M在点N的坐标且不与点A、B重合),顶点P、Q在抛物线上A、B之间部分的图象上,过A、C两点的直线与矩形边MP相交于点E,当矩形MPQN的周长最大时,求△AME的面积;
③当矩形MPQN的周长最大时,在坐标轴上是否存在点D,使得△ACD的面积与②中△AME的面积相等?若存在,求出点D的坐标;若不存在,请说明理由.
(1)求证:不论m为何值,该函数的图象与x轴没有公共点;
(2)当m=1时,将函数y1=-x2-2mx-m2-1的图象向上平移5个单位,得到函数y2=-x2+bx+c的图象,且y2=-x2+bx+c的图象与x轴交于A、B两点(点A在点B的左边),与y轴交于点C,如图所示.
①求点A、B、C的坐标;
②如图,矩形MPQN的顶点M、N在线段AB上(点M在点N的坐标且不与点A、B重合),顶点P、Q在抛物线上A、B之间部分的图象上,过A、C两点的直线与矩形边MP相交于点E,当矩形MPQN的周长最大时,求△AME的面积;
③当矩形MPQN的周长最大时,在坐标轴上是否存在点D,使得△ACD的面积与②中△AME的面积相等?若存在,求出点D的坐标;若不存在,请说明理由.

▼优质解答
答案和解析
(1)二次函数y1=-x2-2mx-m2-1,
△=(-2m)2-4×(-1)×(-m2-1)=-4<0,
∴不论m为何值,该函数的图象与x轴没有公共点;
(2)①把m=1代入抛物线y1=-x2-2mx-m2-1得:y1=-x2-2x-2=-(x+1)2-1,向上平移5个单位得:y2=-(x+1)2+4=-x2-2x+3,
令y=0得,0=-(x+1)2+4,解得:x=1,或x=-3,
∴点A(-3,0),B(1,0),
当x=0时,y=3,
∴点C(0,3),
②如图1:
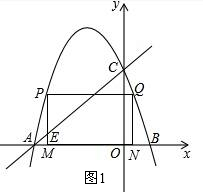
设点N(m,0),则Q(m,-m2-2m+3),
QN=-m2-2m+3,MN=AB-2BN=4-2(1-m)=2m+2,
矩形MPQN的周长=2(-m2-2m+3+2m+2)=-2m2+10,
当m=0时,矩形MPQN的周长有最大值是10,
此时N(0,0),M(-2,0),P(-2,3),Q(0,3),AM=1,OA=3,OC=3,
由题意易证△AEM∽△AOC,得
=
,
∴
=
,解得:EM=1,
∴△AME的面积=
×1×1=
;
③如图2:
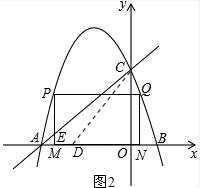
若点D在x轴上,设点D(n,0),AD=|n+3|,此时S△ACD=
,
∴
|n+3|×3=
,解得:n=-
,或n=-
,
此时点D坐标为(-
,0),或(-
,0),
如图3:
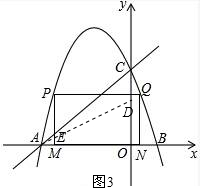
若点D在y轴上,设点D(0,p),CD=|p-3|,此时S△ACD=
,
∴
|p-3|×3=
,解得:p=
,或p=
,
此时点D坐标为:(0,
),或(0,
),
综上所述:△ACD的面积与②中△AME的面积相等时,点D的坐标为:(-
,0),(-
,0),(0,
),(0,
).
△=(-2m)2-4×(-1)×(-m2-1)=-4<0,
∴不论m为何值,该函数的图象与x轴没有公共点;
(2)①把m=1代入抛物线y1=-x2-2mx-m2-1得:y1=-x2-2x-2=-(x+1)2-1,向上平移5个单位得:y2=-(x+1)2+4=-x2-2x+3,
令y=0得,0=-(x+1)2+4,解得:x=1,或x=-3,
∴点A(-3,0),B(1,0),
当x=0时,y=3,
∴点C(0,3),
②如图1:

设点N(m,0),则Q(m,-m2-2m+3),
QN=-m2-2m+3,MN=AB-2BN=4-2(1-m)=2m+2,
矩形MPQN的周长=2(-m2-2m+3+2m+2)=-2m2+10,
当m=0时,矩形MPQN的周长有最大值是10,
此时N(0,0),M(-2,0),P(-2,3),Q(0,3),AM=1,OA=3,OC=3,
由题意易证△AEM∽△AOC,得
| AM |
| AO |
| EM |
| OC |
∴
| 1 |
| 3 |
| EM |
| 3 |
∴△AME的面积=
| 1 |
| 2 |
| 1 |
| 2 |
③如图2:

若点D在x轴上,设点D(n,0),AD=|n+3|,此时S△ACD=
| 1 |
| 2 |
∴
| 1 |
| 2 |
| 1 |
| 2 |
| 10 |
| 3 |
| 8 |
| 3 |
此时点D坐标为(-
| 10 |
| 3 |
| 8 |
| 3 |
如图3:

若点D在y轴上,设点D(0,p),CD=|p-3|,此时S△ACD=
| 1 |
| 2 |
∴
| 1 |
| 2 |
| 1 |
| 2 |
| 10 |
| 3 |
| 8 |
| 3 |
此时点D坐标为:(0,
| 10 |
| 3 |
| 8 |
| 3 |
综上所述:△ACD的面积与②中△AME的面积相等时,点D的坐标为:(-
| 10 |
| 3 |
| 8 |
| 3 |
| 10 |
| 3 |
| 8 |
| 3 |
看了 已知二次函数y1=-x2-2...的网友还看了以下:
spss线性回归怎么看相关系数系数(a) 非标准化系数 标准系数模型 B 标准 误差 试用版 2020-05-15 …
甲乙两人同时从相距900米A.B两地同时出发,甲每分钟300米乙每分钟200米两人经过几分钟相距1 2020-05-22 …
已知f(x)=x^n+a1x^(n-1)+a2x^(n-2)+.+an-1x+an`a后面的是下标 2020-06-19 …
翻译下列短语.1.跑向2.开车逃走3.做某事很惊讶4.停止讲话5.左转进入花园路6.在交通灯出停下 2020-06-21 …
三年级三个班共有300本图书,如果1班向2班借15本,又借给3班21本,则三个班的图书刚好相等,三 2020-07-14 …
向量组线性无关的充分必要条件的问题向量组α1,α2,…,αm线性无关的充分必要条件是().A.向量 2020-07-26 …
如图所示是心脏及其连接的血管结构示意图,请根据图回答:(1)心脏的四个腔中,壁最厚的是[].(2) 2020-07-29 …
近亲婚配使子女的发病风险增高的疾病包括1常显2常隐3伴x显4线粒体遗传5多基因遗传答案是34.为什 2020-07-30 …
求使二阶微分方程离散化的方法.比如方程4y“+6y'+3y+2x+5=0如何求解能使其离散化,就是转 2020-11-28 …
沿水平方向向右做匀变速直线运动的车厢中,悬挂小球的线偏离竖直方向30°角(向左偏)球和车厢相对静止, 2021-01-02 …