如图，在钝角△ABC中，分别以AB和AC为斜边向△ABC的外作等腰直角三角形ABE和等腰直角三角形ACF，FN平分∠AFC交AC于点N，D为BC的中点，DM∥AC交AB于点M，连接DE、DF、EF、EM．对于以下结论：①DM=F

Question

如图，在钝角△ABC中，分别以AB和AC为斜边向△ABC的外作等腰直角三角形ABE和等腰直角三角形ACF，FN平分∠AFC交AC于点N，D为BC的中点，DM∥AC交AB于点M，连接DE、DF、EF、EM．对于以下结论：①DM=FN；②S_{四边形ACDM}=3S_△BDM；③DE=DF；④∠EFD=

(1)/(2)∠EDF．其中正确结论的个数是
（　　）

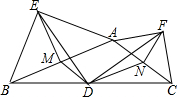
A. 1个

B. 2个

C. 3个

D. 4个

Answer 1

∵D是BC中点，DM∥AC
∴M是AB中点，
∴DM是△ABC的中位线，
∴DM∥AC，且DM=(1)/(2)AC；
∵三角形ABE是等腰直角三角形，FM平分∠AAFC交AC于点N，
∴N是AC的中点，
∴FN=(1)/(2)AC，
又∵DM=(1)/(2)AC，
∴DM=FN，
∴结论①正确；

∵DM∥AC，
∴△MBD∽ABC，
∵DM=(1)/(2)AC，
∴S_△MBD=(1)/(4)S_△ABC，
∴S_{四边形AMDC}=3S_△MBD
∴结论②正确；

∵D是BC中点，DM∥AC，
∴M是AB中点，
∴DM是△ABC的中位线，
∴DM∥AC，且DM=(1)/(2)AC；
∵三角形ACF是等腰直角三角形，N是AC的中点，
∴FN=(1)/(2)AC，
又∵DM=(1)/(2)AC，
∴DM=FN，
∵DM∥AC，DN∥AB，
∴四边形AMDN是平行四边形，
∴∠AMD=∠AND，
又∵∠EMA=∠FNA=90°，
∴∠EMD=∠DNF，
在△EMD和△DNF中，

EM=DN

∠EMD=∠DNF

MD=NF

，
∴△EMD≌△DNF，
∴DE=DF，
∴结论③正确；

设DF与AC交于点K，
∵DM∥AC，
∴∠AKF=∠MDF，
∴∠KFN+∠FNK=∠EDM+∠EDF，
∵△EMD≌△DNF，∠FNK=90°
∴∠EDM=∠DFN，
∴∠EDF=∠FNK=90°，
∴DE⊥DF，
∴结论④正确．
∴正确的结论有4个：①②③④．
故选：D．