早教吧作业答案频道 -->数学-->
阅读材料:如图1,四边形ABCD的对角线AC,BD交于点O,点M是AB边上的一点,过点M分别作ME∥BD,MF∥AC交直线AC,BD于点E,F,显然四边形OEMF是平行四边形.探究发现:(1)当对角线AC,BD满足
题目详情
阅读材料:如图1,四边形ABCD的对角线AC,BD交于点O,点M是AB边上的一点,过点M分别作ME∥BD,MF∥AC交直线AC,BD于点E,F,显然四边形OEMF是平行四边形.
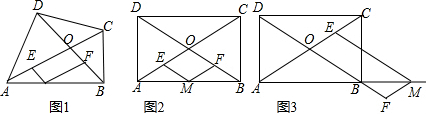
探究发现:
(1)当对角线AC,BD满足___时,四边形OEMF是矩形.
(2)如图2,若四边形ABCD是矩形,且M是AB的中点,判断四边形OEMF是什么特殊的平行四边形,并写出证明过程.
拓展延伸:
(3)如图3,在四边形ABCD为矩形的条件下,若点M是边AB延长线上的一点,此时OA,ME,MF三条线段之间存在怎样的数量关系?并说明理由.

探究发现:
(1)当对角线AC,BD满足___时,四边形OEMF是矩形.
(2)如图2,若四边形ABCD是矩形,且M是AB的中点,判断四边形OEMF是什么特殊的平行四边形,并写出证明过程.
拓展延伸:
(3)如图3,在四边形ABCD为矩形的条件下,若点M是边AB延长线上的一点,此时OA,ME,MF三条线段之间存在怎样的数量关系?并说明理由.
▼优质解答
答案和解析
(1) 要使平行四边形OEMF是矩形,
∴∠AOB=90°,
∴AC⊥BD,
故答案为AC⊥BD.
(2)四边形OEMF是菱形.
证明:
在矩形ABCD中,OA=OB,
∵点M是AB的中点,ME∥BD,MF∥AC,
∴ME=
OB,MF=
OA,
∴ME=MF,
∵四边形OEMF是平行四边形,
∴四边形OEMF是菱形.
(3) MF+OA=ME,
理由:在矩形ABCD中,OA=OB,
∵ME∥BD,MF∥AC,
∴四边形OEMF是平行四边形,
∴MF=EO,
∴∠OAB=∠OBA=∠EMA,
∴EA=EM,
∵MF=OE,
∴MF+OA=ME
∴∠AOB=90°,
∴AC⊥BD,
故答案为AC⊥BD.
(2)四边形OEMF是菱形.
证明:
在矩形ABCD中,OA=OB,
∵点M是AB的中点,ME∥BD,MF∥AC,
∴ME=
| 1 |
| 2 |
| 1 |
| 2 |
∴ME=MF,
∵四边形OEMF是平行四边形,
∴四边形OEMF是菱形.
(3) MF+OA=ME,
理由:在矩形ABCD中,OA=OB,
∵ME∥BD,MF∥AC,
∴四边形OEMF是平行四边形,
∴MF=EO,
∴∠OAB=∠OBA=∠EMA,
∴EA=EM,
∵MF=OE,
∴MF+OA=ME
看了 阅读材料:如图1,四边形AB...的网友还看了以下:
某案件的唯一罪犯锁定在A、B、C、D、E、F六人中.下列四句只有一真:(1)作案者不是A,就是B( 2020-05-16 …
已知B1,B2分别是中心在远点,焦点在x轴上椭圆C的上下顶点,F是C的右焦点,FB1=2,F到C的 2020-05-17 …
A.F,H,C,D,P,A,M,Q,R,S,Y,XB.P,A,C,S,Q,D,F,X,R,H,M,Y 2020-05-26 …
若函数f(x)在点x0处可导,则()是错误的.A.函数f(x)在点x0处有定义B.limf(x)= 2020-06-11 …
设f(x)=x²+bx+c,且f(-1)=f(3),则()A.f(1)>c>f(-1)B.f(1) 2020-06-12 …
(6分)下列A~F是初中化学中的六个实验装置,请按要求填空:(1)A实验试管2中产生的气体是。(2 2020-06-18 …
学数据结构遇到的问题,有6个元素a,b,c,d,e,f依次入栈,下列出栈序列中哪个是不可能的?A) 2020-06-28 …
用一重10N的动滑轮匀速提升重50N的物体,实际工作时拉力F是多少?A.可能是35NB.正好是30 2020-06-30 …
设一组初始记录关键字序列为(Q,H,C,Y,P,A,M,S,R,D,F,X),则按字母升序的第一趟 2020-07-17 …
某中学生物兴趣小组的同学收集到了部分生物图片(如图),请你按下列分类方法将这些生物分类,然后回答有 2020-07-21 …