早教吧作业答案频道 -->数学-->
已知,如图1,直线l与反比例函数y=kx(k>0)位于第一象限的图象相交于A、B两点,并与y轴、x轴分别交于E、F.(1)试判断AE与BF的数量关系并说明理由.(2)如图2,若将直线l绕点A顺时针
题目详情
已知,如图1,直线l与反比例函数y=
(k>0)位于第一象限的图象相交于A、B两点,并与y轴、x轴分别交于E、F.
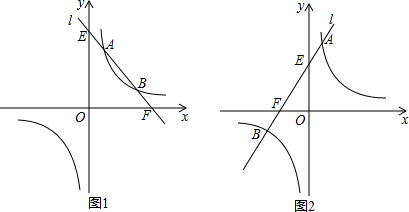
(1)试判断AE与BF的数量关系并说明理由.
(2)如图2,若将直线l绕点A顺时针旋转,使其与反比例函数y=
的另一支图象相交,设交点为B.试判断AE与BF的数量关系是否依然成立?请说明理由.
| k |
| x |

(1)试判断AE与BF的数量关系并说明理由.
(2)如图2,若将直线l绕点A顺时针旋转,使其与反比例函数y=
| k |
| x |
▼优质解答
答案和解析
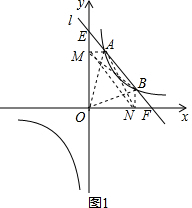 (1)AE=BF,
(1)AE=BF,
理由如下:作AM⊥y轴于M,BN⊥x轴于N,连接MN、OA、OB、BM、AN,
∵AM∥x轴,
∴S△AMN=S△AMO=
,
同理,S△BMN=S△BNO=
,
∴S△AMN=S△BMN,
即A、B两点到MN的距离相等,且A、B位于MN同侧,故AB∥MN,
∴四边形AMNF与BNME均为平行四边形,
∴AM=FN,EM=BN.
又∵∠AME=∠BNF=90°,
在△EMA与△BNF中,
,
∴△EMA≌△BNF,
∴AE=BF;
(2)结论依然成立,AE=BF,
理由: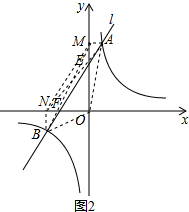 作AM⊥y轴于M,BN⊥x轴于N,连接MN、OA、OB、BM、AN,
作AM⊥y轴于M,BN⊥x轴于N,连接MN、OA、OB、BM、AN,
∵AM∥x轴,
∴S△AMN=S△AMO=
,
同理,S△BMN=S△BNO=
,
∴S△AMN=S△BMN,
即A、B两点到MN的距离相等,且A、B位于MN同侧,故AB∥MN,
∴四边形AMNF与BNME均为平行四边形,
∴AM=FN,EM=BN.
又∵∠AME=∠BNF=90°,
在△EMA与△BNF中,
,
∴△EMA≌△BNF,
∴AE=BF.
 (1)AE=BF,
(1)AE=BF,理由如下:作AM⊥y轴于M,BN⊥x轴于N,连接MN、OA、OB、BM、AN,
∵AM∥x轴,
∴S△AMN=S△AMO=
| k |
| 2 |
同理,S△BMN=S△BNO=
| k |
| 2 |
∴S△AMN=S△BMN,
即A、B两点到MN的距离相等,且A、B位于MN同侧,故AB∥MN,
∴四边形AMNF与BNME均为平行四边形,
∴AM=FN,EM=BN.
又∵∠AME=∠BNF=90°,
在△EMA与△BNF中,
|
∴△EMA≌△BNF,
∴AE=BF;
(2)结论依然成立,AE=BF,
理由:
 作AM⊥y轴于M,BN⊥x轴于N,连接MN、OA、OB、BM、AN,
作AM⊥y轴于M,BN⊥x轴于N,连接MN、OA、OB、BM、AN,∵AM∥x轴,
∴S△AMN=S△AMO=
| k |
| 2 |
同理,S△BMN=S△BNO=
| k |
| 2 |
∴S△AMN=S△BMN,
即A、B两点到MN的距离相等,且A、B位于MN同侧,故AB∥MN,
∴四边形AMNF与BNME均为平行四边形,
∴AM=FN,EM=BN.
又∵∠AME=∠BNF=90°,
在△EMA与△BNF中,
|
∴△EMA≌△BNF,
∴AE=BF.
看了 已知,如图1,直线l与反比例...的网友还看了以下:
如图,正比例函数y=k1x与反比例函数y=x分之k2交于点A如图正比例函数y=k1x与反比例函数y 2020-04-05 …
如果2X=Y,那么X和Y()比例;如果圆的周长一定,那么圆的直径和圆周率()比例如果2X=Y,那么 2020-04-27 …
已知x(20和15)和y(3和7.5)那么x和y成什么比列,如果x是5,y是多少?,如果x是24, 2020-05-13 …
用什么比喻白雪,两个。最好一个体现与白雪相似的动态美,一个描写与白雪的神似如将盐比作白雪。 2020-05-13 …
如果7x=y,那么x和y成()比例.如果3分之y=x分之2(我打的是y比3=2比x),那么x和y成 2020-05-19 …
下面这些题怎么写?都把我弄糊涂了,最好写出怎样判断、分析?题如下:如果Y=8X,X和Y()比例.A 2020-06-12 …
(2013•泸州)如图,已知函数y=43x与反比例函数y=kx(x>0)的图象交于点A.将y=43 2020-08-03 …
如果y与x成正比,y与z成正比,如何证明y与xz(即xz相乘)成正比?如果假设y=ax=bz,那么y 2020-11-01 …
关于什么是正比例什么是反比例.正比例就是,当X越大时,相关的Y越大,如2X=Y反比例正好相反,如2/ 2020-11-28 …
比例问题解答下面这些题怎么写?都把我弄糊涂了,那位数学高手教教我,最好写出怎样判断、分析?谢谢!题如 2020-11-28 …