早教吧作业答案频道 -->数学-->
在Rt△ABC中,∠BAC=90°,D是BC的中点,E是AD的中点,过点A作AF∥BC交BE的延长线于点F.(1)求证:△AEF≌△DEB;(2)证明四边形ADCF是菱形;(3)若AC=4,AB=5,求菱形ADCF的面积.
题目详情
在Rt△ABC中,∠BAC=90°,D是BC的中点,E是AD的中点,过点A作AF∥BC交BE的延长线于点F.
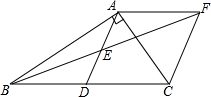
(1)求证:△AEF≌△DEB;
(2)证明四边形ADCF是菱形;
(3)若AC=4,AB=5,求菱形ADCF的面积.

(1)求证:△AEF≌△DEB;
(2)证明四边形ADCF是菱形;
(3)若AC=4,AB=5,求菱形ADCF的面积.
▼优质解答
答案和解析
(1)证明:①∵AF∥BC,
∴∠AFE=∠DBE,
∵E是AD的中点,AD是BC边上的中线,
∴AE=DE,BD=CD,
在△AFE和△DBE中,
,
∴△AFE≌△DBE(AAS);
(2)证明:由(1)知,△AFE≌△DBE,则AF=DB.
∵DB=DC,
∴AF=CD.
∵AF∥BC,
∴四边形ADCF是平行四边形,
∵∠BAC=90°,D是BC的中点,E是AD的中点,
∴AD=DC=
BC,
∴四边形ADCF是菱形;
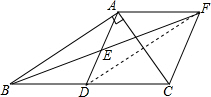
(3)连接DF,
∵AF∥BD,AF=BD,
∴四边形ABDF是平行四边形,
∴DF=AB=5,
∵四边形ADCF是菱形,
∴S菱形ADCF=
AC▪DF=
×4×5=10.
∴∠AFE=∠DBE,
∵E是AD的中点,AD是BC边上的中线,
∴AE=DE,BD=CD,
在△AFE和△DBE中,
|
∴△AFE≌△DBE(AAS);
(2)证明:由(1)知,△AFE≌△DBE,则AF=DB.
∵DB=DC,
∴AF=CD.
∵AF∥BC,
∴四边形ADCF是平行四边形,
∵∠BAC=90°,D是BC的中点,E是AD的中点,
∴AD=DC=
| 1 |
| 2 |
∴四边形ADCF是菱形;

(3)连接DF,
∵AF∥BD,AF=BD,
∴四边形ABDF是平行四边形,
∴DF=AB=5,
∵四边形ADCF是菱形,
∴S菱形ADCF=
| 1 |
| 2 |
| 1 |
| 2 |
看了 在Rt△ABC中,∠BAC=...的网友还看了以下:
VB程序设计中关于函数过程中的题目定义一个Function(函数)过程,求长方体的面积S=a*b( 2020-05-14 …
已知:如图,四边形ABCD是菱形,过AB的中点E作AC的垂线EF,交AD于点M,交CD的延长线于已 2020-05-16 …
已知:如图,四边形ABCD是菱形,过AB的中点E作AC的垂线EF,交AD于点M,交CD的延长线于点 2020-05-16 …
求一篇高中作文.800字以内阅读下面文字,按要求写一篇文章.(60分)水从高原流下,自西向东,流入 2020-06-04 …
1.√(x+1)2+(y+1)2=√(x-3)2+(y-7)2 整理 得x+2y-7=0 求中间详 2020-06-27 …
7.1mol理想气体经历如图所示的abc过程,其中a→b为等压过程,b→c为等体过程,且已知Ta= 2020-07-09 …
1mol理想气体经历如图所示的abc过程,其中a→b为等压过程,b→c为等体过程,且已知Ta=Tc 2020-07-09 …
1mol理想气体经历如图所示的abc过程,其中a→b为等压过程,b→c为等体过程,且已知Ta=Tc 2020-07-09 …
求解析几何中的轨迹方程过椭圆上一点P,引短轴的平行线,又作P点的切线,求过椭圆中心垂直於切线的直线 2020-08-02 …
1求一个由十个数构成的一维数组的平均值,并求出低于平均值的数的和.2.编写一求圆面积的函数过程,在 2020-08-03 …