如图是两块完全一样的含30°角的三角板，分别记作△ABC和△A1B1C1，现将两块三角板重叠在一起，高较长直角边的中点为M，绕中点M转动上面的三角板ABC，直角顶点C恰好落在三角板△A1B1C1的斜

Question

如图是两块完全一样的含30°角的三角板，分别记作△ABC和△A₁B₁C₁，现将两块三角板重叠在一起，高较长直角边的中点为M，绕中点M转动上面的三角板ABC，直角顶点C恰好落在三角板△A₁B₁C₁的斜边A₁B₁上．当∠A=30°，B₁C=2时，则此时AB的长为（　　）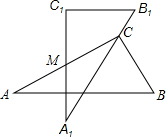

A. 6

B. 8

C. 9

D. 10

Answer 1

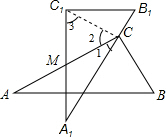连接C₁C，
∵M是AC的中点，△ABC，△A₁B₁C₁是两块完全一样的含30°角三角板重叠在一起的，
∴AM=CM=(1)/(2)A₁C₁，
即CM=AA₁M=C₁M，
∴∠A₁=∠1，∠2=∠3，
∴A₁+∠3=∠1+∠2=90°=∠A₁CC₁，
∴△B₁C₁C为直角三角形，
∵∠A₁=30°，
∴∠B₁=60°，
∴∠B₁C₁C=30°，
∴BC=B₁C₁=2B₁C=4，
∵∠A=30°，
∴AB=2BC=8．
故答案为B．