早教吧作业答案频道 -->数学-->
如图,在▱ABCD中,AB=2,BC=4,∠ABC=60°,E,F分别是BC,AD上的两点,且BE=DF,连AE,BF,DE,CF分别交于点G,H.(1)求证:四边形GEHF是平行四边形.(2)若E,F分别是BC,AD上的两个动点,设B
题目详情
如图,在▱ABCD中,AB=2,BC=4,∠ABC=60°,E,F分别是BC,AD上的两点,且BE=DF,连AE,BF,DE,CF分别交于点G,H.
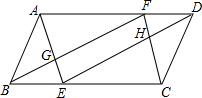
(1)求证:四边形GEHF是平行四边形.
(2)若E,F分别是BC,AD上的两个动点,设BE=DF=x,试推断当x等于多少时,四边形GEHF是矩形.

(1)求证:四边形GEHF是平行四边形.
(2)若E,F分别是BC,AD上的两个动点,设BE=DF=x,试推断当x等于多少时,四边形GEHF是矩形.
▼优质解答
答案和解析
(1)证明:∵四边形ABCD是平行四边形,
∴AD∥BC,AD=BC,
∴BE∥DF,
∵BE=DF,
∴四边形FBED是平行四边形,
∴BF∥ED,即GF∥EH,
同理:四边形AECF是平行四边形,
∴AE∥FC,
即GE∥FH,
∴四边形GEHF是平行四边形;
(2) 当AE平分∠BAD,CF平分∠BCD时,BE=DF=2,四边形GEHF是矩形;理由如下:
∵四边形ABCD是平行四边形,
∴∠BAD=180°-∠ABC=180°-60°=120°,
∴∠ABC=∠BAC=∠AEB=60°,
∴△ABE是等边三角形,
∴BE=DF=AB=2,
∴AF=CE=BC-BE=4-2=2,
∴AB=AF,
∴∠ABG=∠AFG=30°,
∴∠AGB=90°,
∴∠EGF=90°,
∴四边形GEHF是矩形;
即当x=2时,四边形GEHF是矩形.
∴AD∥BC,AD=BC,
∴BE∥DF,
∵BE=DF,
∴四边形FBED是平行四边形,
∴BF∥ED,即GF∥EH,
同理:四边形AECF是平行四边形,
∴AE∥FC,
即GE∥FH,
∴四边形GEHF是平行四边形;
(2) 当AE平分∠BAD,CF平分∠BCD时,BE=DF=2,四边形GEHF是矩形;理由如下:
∵四边形ABCD是平行四边形,
∴∠BAD=180°-∠ABC=180°-60°=120°,
∴∠ABC=∠BAC=∠AEB=60°,
∴△ABE是等边三角形,
∴BE=DF=AB=2,
∴AF=CE=BC-BE=4-2=2,
∴AB=AF,
∴∠ABG=∠AFG=30°,
∴∠AGB=90°,
∴∠EGF=90°,
∴四边形GEHF是矩形;
即当x=2时,四边形GEHF是矩形.
看了 如图,在▱ABCD中,AB=...的网友还看了以下:
反比例函数的一道题已知点A,B两点是反比例函数y=2/x(x>0)的图像上任意两点(A点在B点的上 2020-05-17 …
如图,AB是一条圆形环湖路的直径,小张在A点、小王在B点同时沿湖边跑步.他们沿如图所示方向匀速跑步 2020-06-06 …
光滑水平面AB与竖直面内的粗糙半圆形导轨在B点平滑连接,导轨半径为R,一个质量m的小物块在A点以V 2020-06-20 …
如图是一个圆形花圃的平面图形,A,B是这个圆形花圃直径的两端.李明和张亮在这个圆形花圃里玩游戏.李 2020-07-03 …
一个圆形花圃,A,B是这个花圃直径的两端,李明和张亮在花圃上玩游戏,李在A点,张在B点,同时出发, 2020-07-03 …
某驾培中心训练场有一段圆弧形坡道如图所示,将同一辆车物后停放在a点和b点。下述分析和比较正确的是A 2020-07-11 …
如图所示,斜面轨道AB与水平面之间的夹角,BD为半径R=4m的圆弧形轨道,且B点与D点在同一水平面上 2020-11-01 …
如图所示,在直角三角形ABC中,∠A=60°,∠B=90°,在A点放置一个点电荷,该点电荷形成的电场 2020-11-03 …
AB是圆形跑道直径的两端,小张在A点与小王在B点同时出发反向行走,他们在C点第一次相遇,C点离A点8 2020-11-25 …
在图-2中,当某商品的价格停留在A点或B点时,下列说法中正确的是:图-2①在A点形成通货膨胀,在B点 2020-12-05 …