早教吧作业答案频道 -->数学-->
如图:已知A(a,0)、B(0,b),且a、b满足(a-2)2+|2b-4|=0.(1)如图1,求△AOB的面积;(2)如图2,点C在线段AB上(不与A、B重合)移动,AB⊥BD,且∠COD=45°,猜想线段AC、BD、CD之间的数
题目详情
如图:已知A(a,0)、B(0,b),且a、b满足(a-2)2+|2b-4|=0.
(1)如图1,求△AOB的面积;
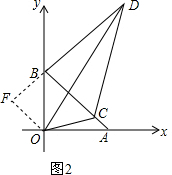
(2)如图2,点C在线段AB上(不与A、B重合)移动,AB⊥BD,且∠COD=45°,猜想线段AC、BD、CD之间的数量关系并证明你的结论;
(3)如图3,若P为x轴上异于原点O和点A的一个动点,连接PB,将线段PB绕点P顺时针旋转90°至PE,直线AE交y轴Q,点Q,当P点在x轴上移动时,线段BE和线段BQ中,请判断哪条线段长为定值,并求出该定值.
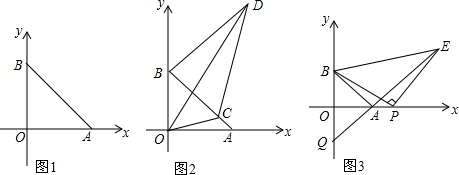
(1)如图1,求△AOB的面积;
(2)如图2,点C在线段AB上(不与A、B重合)移动,AB⊥BD,且∠COD=45°,猜想线段AC、BD、CD之间的数量关系并证明你的结论;
(3)如图3,若P为x轴上异于原点O和点A的一个动点,连接PB,将线段PB绕点P顺时针旋转90°至PE,直线AE交y轴Q,点Q,当P点在x轴上移动时,线段BE和线段BQ中,请判断哪条线段长为定值,并求出该定值.

▼优质解答
答案和解析
(1) ∵ (a-2)2+|2b-4|=0,∴a-2=0,2b-4=0,
(a-2)2+|2b-4|=0,∴a-2=0,2b-4=0,
∴a=2,b=2,
∴A(2,0)、B(0,2),
∴OA=2,OB=2,
∴△AOB的面积=
×2×2=2;
(2)证明:将△AOC绕点O逆时针旋转90°得到△OBF,
∵∠OAC=∠OBF=∠OBA=45°,∠DBA=90°,
∴∠BDF=180°,
∵∠DOC=45°,∠AOB=90°,
∴∠BOD+∠AOC=45°,
∴∠FOD=∠BOF+∠BOD=∠BOD+∠AOC=45°,
在△ODF与△ODC中,
,
∴△ODF≌△ODC,
∴DC=DF=DB+BF=DB+DC;
(3)BQ是定值,作EF⊥OA于F,在FE上截取PF=FD,
∵∠BAO=∠PDF=45°,
∴∠PAB=∠PD,E=135°,
∴∠BPA+∠EPF=90°∠EPF+∠PED=90°,
∴∠BPA=∠PED,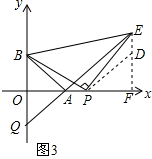
在△PBA与△EPD中,
,
∴△PBA≌EPD,
∴AP=ED,
∴FD+ED=PF+AP,
即:FE=FA,
∴∠FEA=∠FAE=45°,
∴∠QAO=∠EAF=∠OQA=45°,
∴OA=OQ=2,
∴BQ=4.
 (a-2)2+|2b-4|=0,∴a-2=0,2b-4=0,
(a-2)2+|2b-4|=0,∴a-2=0,2b-4=0,∴a=2,b=2,
∴A(2,0)、B(0,2),
∴OA=2,OB=2,
∴△AOB的面积=
| 1 |
| 2 |
(2)证明:将△AOC绕点O逆时针旋转90°得到△OBF,
∵∠OAC=∠OBF=∠OBA=45°,∠DBA=90°,
∴∠BDF=180°,
∵∠DOC=45°,∠AOB=90°,
∴∠BOD+∠AOC=45°,
∴∠FOD=∠BOF+∠BOD=∠BOD+∠AOC=45°,
在△ODF与△ODC中,
|
∴△ODF≌△ODC,
∴DC=DF=DB+BF=DB+DC;
(3)BQ是定值,作EF⊥OA于F,在FE上截取PF=FD,
∵∠BAO=∠PDF=45°,
∴∠PAB=∠PD,E=135°,
∴∠BPA+∠EPF=90°∠EPF+∠PED=90°,
∴∠BPA=∠PED,

在△PBA与△EPD中,
|
∴△PBA≌EPD,
∴AP=ED,
∴FD+ED=PF+AP,
即:FE=FA,
∴∠FEA=∠FAE=45°,
∴∠QAO=∠EAF=∠OQA=45°,
∴OA=OQ=2,
∴BQ=4.
看了 如图:已知A(a,0)、B(...的网友还看了以下:
一段粗细不均匀的木棍如图所示,支在某点恰好平衡,若在该处将木棍截成两段,则所分成两段的重量必定是A 2020-04-27 …
爸爸将一条大鲤鱼分成前、中、后三段.中段重量恰好比前、后段的重量的和少1千克.后段重量等于中段重量 2020-05-13 …
爸爸把钓来的一条大鲤鱼分成前、中、后三段,中段的重量恰好比前、后两段重量的和少1千克,后段重量等于 2020-05-14 …
两道数学应用题1爸爸把钓来的一条大鲤鱼分成前、中、后三段,中段的重量恰好比前、后两段重量的和少1千 2020-05-20 …
爸爸把钓来的一条大鲤鱼分成前、中、后三段,中段的重量恰好比前、后两段重量的和少1千克,后段重量等于 2020-06-19 …
爸爸将钓来的一条大鲤鱼分成前中后三段.中段重量恰好比前后两段重量的和少1千克,后段重量等于中段重量 2020-06-19 …
爸爸把钓来的一条大鲤鱼分成前、中、后三段,中段的重量恰好比前、后两段重量的和少1千克,后段重量等于 2020-06-19 …
已知数轴上A、B两点所表示的数分别为a和b.(1)如图,a=-1,b=7时①求线段AB的长;②若点 2020-07-30 …
如图,数轴上A,B两点所表示的数互为倒数,则关于原点的说法正确的是()A.一定在点A的左侧B.一定与 2020-11-08 …
如图,已知线段AB=a(a>1),线段CD=1,线段CD在线段AB上由点A向点B从左向右移动(点C不 2021-01-12 …