早教吧作业答案频道 -->数学-->
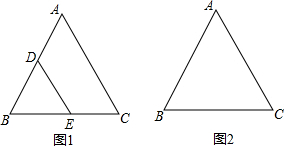
已知,在等边△ABC中,AB=23,D,E分别是AB,BC的中点(如图1).若将△BDE绕点B逆时针旋转,得到△BD1E1,设旋转角为α(0°<α<180°),记射线CE1与AD1
题目详情
已知,在等边△ABC中,AB=2
,D,E分别是AB,BC的中点(如图1).若将△BDE绕点B逆时针旋转,得到△BD1E1,设旋转角为α(0°<α<180°),记射线CE1与AD1的交点为P.
(1)判断△BDE的形状;
(2)在图2中补全图形,
①猜想在旋转过程中,线段CE1与AD1的数量关系并证明;
②求∠APC的度数;
(3)点P到BC所在直线的距离的最大值为___.(直接填写结果)
| | 3 |
(1)判断△BDE的形状;
(2)在图2中补全图形,
①猜想在旋转过程中,线段CE1与AD1的数量关系并证明;
②求∠APC的度数;
(3)点P到BC所在直线的距离的最大值为___.(直接填写结果)

▼优质解答
答案和解析
(1)∵D,E分别是AB,BC的中点,
∴DE=
BC,BD=
BA,
∵△ABC为等边三角形,
∴∠B=60°,BA=BC,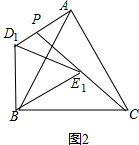
∴BD=BE,
∴△BDE为等边三角形;
(2)①CE1=AD1.理由如下:
∵△BDE绕点B逆时针旋转,得到△BD1E1,
∴△BD1E1为等边三角形,
∴BD1=BE1,∠D1BE1=60°,
而∠ABC=60°,
∴∠ABD1=∠CBE1,
∴△ABD1可由△CBE1绕点B逆时针旋转得到,
∴CE1=AD1;
②∵△ABD1可由△CBE1绕点B逆时针旋转得到,
∴∠BAD1=∠BCE1,
∴∠APC=∠ABC=60°;
(3)∵∠APC=∠D1BE1=60°,
∴点P、D1、B、E1共圆,
∴当BP⊥BC时,点P到BC所在直线的距离的最大值,此时点E1在AB上,
在Rt△PBC中,PB=
AB=
×2
=2,
∴点P到BC所在直线的距离的最大值为2.
故答案为2.
∴DE=
| 1 |
| 2 |
| 1 |
| 2 |
∵△ABC为等边三角形,
∴∠B=60°,BA=BC,

∴BD=BE,
∴△BDE为等边三角形;
(2)①CE1=AD1.理由如下:
∵△BDE绕点B逆时针旋转,得到△BD1E1,
∴△BD1E1为等边三角形,
∴BD1=BE1,∠D1BE1=60°,
而∠ABC=60°,
∴∠ABD1=∠CBE1,
∴△ABD1可由△CBE1绕点B逆时针旋转得到,
∴CE1=AD1;
②∵△ABD1可由△CBE1绕点B逆时针旋转得到,
∴∠BAD1=∠BCE1,
∴∠APC=∠ABC=60°;
(3)∵∠APC=∠D1BE1=60°,
∴点P、D1、B、E1共圆,
∴当BP⊥BC时,点P到BC所在直线的距离的最大值,此时点E1在AB上,
在Rt△PBC中,PB=
| ||
| 3 |
| ||
| 3 |
| 3 |
∴点P到BC所在直线的距离的最大值为2.
故答案为2.
看了 已知,在等边△ABC中,AB...的网友还看了以下:
已知a*5/6=8/5*b=c*3/2=d-150%,且a,b,c都不等于0,则a,b,c,d中最 2020-04-07 …
已知椭圆T的方程为x^2/a^2+y^2/b^2=1(a>b>0),A(0,b),B(0,-b)和 2020-04-27 …
1.m-2的相反数是6,那么m的值是( ).A.4 B.-4 C.8 D.-82.已知|m+3|+ 2020-05-16 …
已知a+b+c=H a+b+e=J a+d+e=K b+c+d=M c+d+e=N 求a=?b=? 2020-05-16 …
在直角坐标系中,已知点A(-2.0),B(0,4)C(0.3).过C作直线交X轴于D.使以D.O. 2020-06-02 …
初三比例式计算.如题.已知a/b=c/d(bd不等于0).判断下列比例式是否成立.并说明理由.a- 2020-06-10 …
以下程序的执行结果是20为什么?#includemain(){ina,b,c,d,x;a=c=0; 2020-06-26 …
集合的运算1.已知A={1,2,3,4},B={3,4,5},求A交集B,A并集B.2.已知A={ 2020-07-30 …
已知平面上三点A(0,0),B(10,0),D(0,6),过原点的直线将三角形ABD分成面积比为2: 2020-11-03 …
已知四边形ABCD的边长依次是a、b、c、d,且a(a+b)-(ac+bc)=0,(b²+bc)-d 2020-12-10 …