如图，正方形OABC的边长为6，A，C分别位于x轴、y轴上，点P在AB上，CP交OB于点Q，函数y=kx的图象经过点Q，若S△BPQ=14S△OQC，则k的值为（）A.-12B.12C.16D.18

Question

如图，正方形OABC的边长为6，A，C分别位于x轴、y轴上，点P在AB上，CP交OB于点Q，函数y=

(k)/(x)的图象经过点Q，若S_△BPQ=(1)/(4)S_△OQC，则k的值为（　　）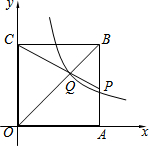

A. -12

B. 12

C. 16

D. 18

Answer 1

∵PB∥OC（四边形OABC为正方形），
∴△PBQ∽△COQ，
∴(S△BPQ)/(S△OQC)=((PB)/(OC))2=(1)/(4)，
∴PB=PA=(1)/(2)OC=3．
∵正方形OABC的边长为6，
∴点C（0，6），点P（6，3），直线OB的解析式为y=x①，
∴设直线CP的解析式为y=ax+6，
∵点P（6，3）在直线CP上，
∴3=6a+6，解得：a=-(1)/(2)，
故直线CP的解析式为y=-(1)/(2)x+6②．
联立①②得：

y=x

y=-(1)/(2)x+6

，
解得：

x=4

y=4

，
∴点Q的坐标为（4，4）．
将点Q（4，4）代入y=(k)/(x)中，得：
4=(k)/(4)，解得：k=16．
故选C．