早教吧作业答案频道 -->数学-->
如图,在等腰△ABC中,AB=AC,点P为底边BC上一动点,连接AP,在AP左侧作等腰△APD,使PA=PD,∠APD=∠BAC,连接BD.(1)如图①,若∠APD=∠BAC=60°,求证:△ABD≌△ACP;(2)如图②,若∠APD=∠BA
题目详情
如图,在等腰△ABC中,AB=AC,点P为底边BC上一动点,连接AP,在AP左侧作等腰△APD,使PA=PD,∠APD=∠BAC,连接BD.
(1)如图①,若∠APD=∠BAC=60°,求证:△ABD≌△ACP;
(2)如图②,若∠APD=∠BAC=90°,AB=2,当点P由点C运动到点B时:
①∠PBD的大小是否为定值?若为定值,求出其大小,若发生变化,请说明理由;
②求出点D运动的路径长度
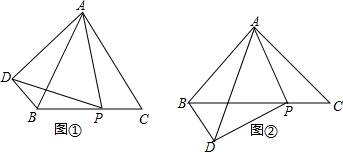
(1)如图①,若∠APD=∠BAC=60°,求证:△ABD≌△ACP;
(2)如图②,若∠APD=∠BAC=90°,AB=2,当点P由点C运动到点B时:
①∠PBD的大小是否为定值?若为定值,求出其大小,若发生变化,请说明理由;
②求出点D运动的路径长度

▼优质解答
答案和解析
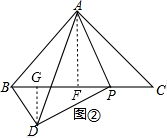 (1)如图①,∵∠BAC=60°,AB=AC,
(1)如图①,∵∠BAC=60°,AB=AC,
∴△ABC等边三角形,
同理得△APD也是等边三角形,
∴AD=AP,∠DAP=60°,
∴∠DAB+∠BAP=∠CAP+∠BAP,
∴∠DAB=∠CAP,
∴△ABD≌△ACP;
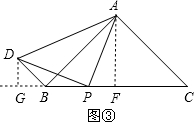 (2)①∠PBD的大小会发生变化,过A作AF⊥BC,交BC于F,则F是BC的中点,
(2)①∠PBD的大小会发生变化,过A作AF⊥BC,交BC于F,则F是BC的中点,
i)当点P在FC上运动时,∠PBD=45°,如图②,理由是:
过点D作DG⊥BC于G,
∵∠APF+∠DPG=90°,∠GDP+∠DPG=90°,
∴∠APF=∠GDP,
∵∠AFP=∠DGP=90°,AP=PD,
∴△AFP≌△PGD,
∴AF=PG,PF=GD,
∵AF=BF,
∴BF=PG,
∴BF-FG=PG-FG,
即BG=PF,
∴BG=GD,
∴△BGD是等腰直角三角形,
∴∠PBD=45°,
ii)当点P与中点F重合时,∠PBD=0°,
iii)当点P在BF上运动时,∠PBD=135°,如图③,
过点D作DG⊥BC,交CB的延长线于点G,
同理得△APF≌△PDG,
∴AF=PG,PF=DG,
∴PG=BF,
∴BG=PF=DG,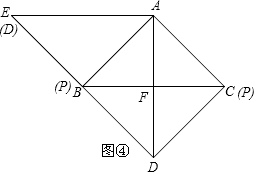
∴△BDG是等腰直角三角形,
∴∠GBD=45°,
∴∠PBD=135°;
②如图④,点D运动的路径是从点D到点E,
当点P在点C时,设AD交BC于F,
∵△APD与△ABC都是等腰直角三角形,
∴AD⊥BC,
当点P运动到点B时,由∠APD=90°得∠ABE=90°,
∵∠ABC=45°,∠CBD=45°,
∴∠EBD=180°,
∴E、B、D在同一直线上,
由题意得:△ADE是等腰直角三角形,
∵AB=2,
∴ED=2AB=4,
∴点D运动的路径长度为4.
 (1)如图①,∵∠BAC=60°,AB=AC,
(1)如图①,∵∠BAC=60°,AB=AC,∴△ABC等边三角形,
同理得△APD也是等边三角形,
∴AD=AP,∠DAP=60°,
∴∠DAB+∠BAP=∠CAP+∠BAP,
∴∠DAB=∠CAP,
∴△ABD≌△ACP;
 (2)①∠PBD的大小会发生变化,过A作AF⊥BC,交BC于F,则F是BC的中点,
(2)①∠PBD的大小会发生变化,过A作AF⊥BC,交BC于F,则F是BC的中点,i)当点P在FC上运动时,∠PBD=45°,如图②,理由是:
过点D作DG⊥BC于G,
∵∠APF+∠DPG=90°,∠GDP+∠DPG=90°,
∴∠APF=∠GDP,
∵∠AFP=∠DGP=90°,AP=PD,
∴△AFP≌△PGD,
∴AF=PG,PF=GD,
∵AF=BF,
∴BF=PG,
∴BF-FG=PG-FG,
即BG=PF,
∴BG=GD,
∴△BGD是等腰直角三角形,
∴∠PBD=45°,
ii)当点P与中点F重合时,∠PBD=0°,
iii)当点P在BF上运动时,∠PBD=135°,如图③,
过点D作DG⊥BC,交CB的延长线于点G,
同理得△APF≌△PDG,
∴AF=PG,PF=DG,
∴PG=BF,
∴BG=PF=DG,

∴△BDG是等腰直角三角形,
∴∠GBD=45°,
∴∠PBD=135°;
②如图④,点D运动的路径是从点D到点E,
当点P在点C时,设AD交BC于F,
∵△APD与△ABC都是等腰直角三角形,
∴AD⊥BC,
当点P运动到点B时,由∠APD=90°得∠ABE=90°,
∵∠ABC=45°,∠CBD=45°,
∴∠EBD=180°,
∴E、B、D在同一直线上,
由题意得:△ADE是等腰直角三角形,
∵AB=2,
∴ED=2AB=4,
∴点D运动的路径长度为4.
看了 如图,在等腰△ABC中,AB...的网友还看了以下:
将证券划分为原生证券和衍生证券所依据的分类标志是( )。A.证券发行主体B.证券权益关系C.证券收 2020-05-17 …
在下列选项中,属于我国法定的证据种类的有( )。 A.直接证据 B.间接证据 C.证人证言 2020-05-18 …
证券中介机构是指( )。A.证券发行人和投资者 B.证券经营机构和证券服务机构C.证券协会 D.证券 2020-05-21 …
在证券市场中,包销或代销证券的经营机构称为( )。A.证券承销商B.证券经纪商C.证券自营商D.证券 2020-05-30 …
两道集合论的题1设ABC是全集U的任意子集.a)若A∩B=A∩C,A∩B=~A∩C,证明:B=Cb 2020-06-07 …
全等三角形的数学题1.AB=AC.BD=CE/角B=角C.证明:AD=AE2.AB//CD.点C是 2020-06-27 …
1、商业银行不动用本身资金,为顾客提供的各类服务的业务是?A负债业务B证券业务C中间业务D同业拆借 2020-07-25 …
下列说法正确的是()A.命题一定是正确的B.不正确的判断就不是命题C.公理都是真命题D.真命题都是 2020-07-30 …
(急)一道基本不等式证明题(高一数学)证明bc/a+ac/b+ab/c≥a+b+c证明:(请看我的 2020-08-03 …
证明填空:如图,已知直线b∥c,a⊥b求证:a⊥c证明:∵a⊥b(已知)∴∠1=90°()又b∥c( 2020-11-02 …