早教吧作业答案频道 -->数学-->
在菱形ABCD和正三角形BGF中,∠ABC=60°,P是DF的中点,连接PG、PC.(1)如图1,当点G在BC边上时,若AB=10,BF=4,求PG的长;(2)如图2,当点F在AB的延长线上时,线段PC、PG有怎样的数量关系,
题目详情
在菱形ABCD和正三角形BGF中,∠ABC=60°,P是DF的中点,连接PG、PC.
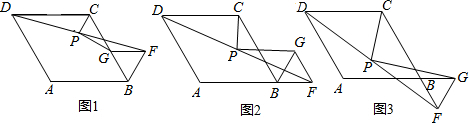
(1)如图1,当点G在BC边上时,若AB=10,BF=4,求PG的长;
(2)如图2,当点F在AB的延长线上时,线段PC、PG有怎样的数量关系,写出你的猜想;并给予证明.
(3)如图3,当点F在CB的延长线上时,(2)问中关系还成立吗?写出你的猜想,并给予证明.

(1)如图1,当点G在BC边上时,若AB=10,BF=4,求PG的长;
(2)如图2,当点F在AB的延长线上时,线段PC、PG有怎样的数量关系,写出你的猜想;并给予证明.
(3)如图3,当点F在CB的延长线上时,(2)问中关系还成立吗?写出你的猜想,并给予证明.
▼优质解答
答案和解析
(1) 如图1:
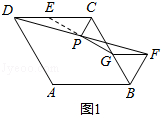
延长GP交DC于点E,
利用△PED≌△PGF,得出PE=PG,DE=FG,
∵△BGF是等边三角形,
∴FG=BG,
又∵四边形ABCD是菱形,
∴CD=CB,
∴CE=CG,
∴CP是EG的中垂线,在Rt△CPG中,∠PCG=60°,
∵AB=10,BF=4;
∴CG=6
∴PG=3
(2)如图2,
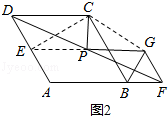
证明:延长GP交DA于点E,连接EC,GC,
∵∠ABC=60°,△BGF正三角形
∴GF∥BC∥AD,
∴∠EDP=∠GFP,
在△DPE和△FPG中
∴△DPE≌△FPG(ASA)
∴PE=PG,DE=FG=BG,
∵∠CDE=∠CBG=60°,CD=CB,
在△CDE和△CBG中,
∴△CDE≌△CBG(SAS)
∴CE=CG,∠DCE=∠BCG,
∴∠ECG=∠DCB=120°,
∵PE=PG,
∴CP⊥PG,∠PCG=
∠ECG=60°
∴PG=
PC.
(3)猜想:PG=
PC.
证明:如图3,
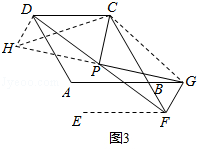
延长GP到H,使PH=PG,连接CH,CG,DH,作FE∥DC
∵P是线段DF的中点,
∴FP=DP,
∵∠GPF=∠HPD,
∴△GFP≌△HDP,
∴GF=HD,∠GFP=∠HDP,
∵∠GFP+∠PFE=120°,∠PFE=∠PDC,
∴∠CDH=∠HDP+∠PDC=120°,
∵四边形ABCD是菱形,
∴CD=CB,∠ADC=∠ABC=60°,点A、B、G又在一条直线上,
∴∠GBC=120°,
∵△BFG是等边三角形,
∴GF=GB,
∴HD=GB,
∴△HDC≌△GBC,
∴CH=CG,∠DCH=∠BCG,
∴∠DCH+∠HCB=∠BCG+∠HCB=120°,即∠HCG=120°
∵CH=CG,PH=PG,
∴PG⊥PC,∠GCP=∠HCP=60°,
∴PG=
PC.

延长GP交DC于点E,
利用△PED≌△PGF,得出PE=PG,DE=FG,
∵△BGF是等边三角形,
∴FG=BG,
又∵四边形ABCD是菱形,
∴CD=CB,
∴CE=CG,
∴CP是EG的中垂线,在Rt△CPG中,∠PCG=60°,
∵AB=10,BF=4;
∴CG=6
∴PG=3
| 3 |
(2)如图2,

证明:延长GP交DA于点E,连接EC,GC,
∵∠ABC=60°,△BGF正三角形
∴GF∥BC∥AD,
∴∠EDP=∠GFP,
在△DPE和△FPG中
|
∴△DPE≌△FPG(ASA)
∴PE=PG,DE=FG=BG,
∵∠CDE=∠CBG=60°,CD=CB,
在△CDE和△CBG中,
|
∴△CDE≌△CBG(SAS)
∴CE=CG,∠DCE=∠BCG,
∴∠ECG=∠DCB=120°,
∵PE=PG,
∴CP⊥PG,∠PCG=
| 1 |
| 2 |
∴PG=
| 3 |
(3)猜想:PG=
| 3 |
证明:如图3,

延长GP到H,使PH=PG,连接CH,CG,DH,作FE∥DC
∵P是线段DF的中点,
∴FP=DP,
∵∠GPF=∠HPD,
∴△GFP≌△HDP,
∴GF=HD,∠GFP=∠HDP,
∵∠GFP+∠PFE=120°,∠PFE=∠PDC,
∴∠CDH=∠HDP+∠PDC=120°,
∵四边形ABCD是菱形,
∴CD=CB,∠ADC=∠ABC=60°,点A、B、G又在一条直线上,
∴∠GBC=120°,
∵△BFG是等边三角形,
∴GF=GB,
∴HD=GB,
∴△HDC≌△GBC,
∴CH=CG,∠DCH=∠BCG,
∴∠DCH+∠HCB=∠BCG+∠HCB=120°,即∠HCG=120°
∵CH=CG,PH=PG,
∴PG⊥PC,∠GCP=∠HCP=60°,
∴PG=
| 3 |
看了 在菱形ABCD和正三角形BG...的网友还看了以下:
小明帮着妈妈提着3kg的大米,爬上10米高的楼层,用时1分钟.(g取10N/kg)求:(1)大米受 2020-04-07 …
lingo程序哪儿错了?MODEL:sets:Quarters/1..4/:a,k,d,c,t,p 2020-05-13 …
matlab solve函数变量问题clcP=[0.9110 0.6777 0.7706 ];D= 2020-05-16 …
有一只瓶子,装满酒精后总质量为600g,装满植物油后总质量为660g,试求(1)瓶子的质量(2)瓶 2020-05-17 …
密度一题求解测得量筒质量为G,装满醋的量筒质量为G1,装满水的量筒质量为G2,已知水密度为p水,求 2020-05-19 …
化学平衡常数与投料有关么.我自己想的.对于反应温度不变M(g)+N(g)=P(g)+Q(g)一起始 2020-06-24 …
对于反应CO2(g)+4H2(g)=CH4(g)+2H2O(g),已经算出来了1000K时的标准平 2020-07-22 …
有一道题麻烦各位说下,已知线段MN和它上面的一点P,G为MP的中点,H为PN的点,MP=10cm, 2020-07-22 …
errorC2059:syntaxerror:'['#includeusingnamespaces 2020-07-23 …
电车m=30kg质量为M=70kg的人骑车所受阻力为总重的0.02倍g=10求由静止开始以a=0.3 2020-10-31 …