早教吧作业答案频道 -->数学-->
已知AD是等边△ABC的高,F为AC边上的一个动点(不与A、C重合),BF与AD相交于点E,连接CE.(1)求证:BE=CE;(2)当△AEF是以为腰的等腰三角形时,求∠ECD的度数;(3)作∠FEG=120°,交
题目详情
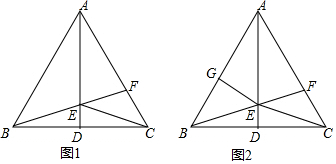
已知AD是等边△ABC的高,F为AC边上的一个动点(不与A、C重合),BF与AD相交于点E,连接CE.
(1)求证:BE=CE;
(2)当△AEF是以___为腰的等腰三角形时,求∠ECD的度数;
(3)作∠FEG=120°,交AB于点G,猜想EF、EG的数量关系并说明理由.
(1)求证:BE=CE;
(2)当△AEF是以___为腰的等腰三角形时,求∠ECD的度数;
(3)作∠FEG=120°,交AB于点G,猜想EF、EG的数量关系并说明理由.

▼优质解答
答案和解析
 (1)∵AD是等边△ABC的高,
(1)∵AD是等边△ABC的高,
∴AD是BC的垂直平分线,
∵点E在AD上,
∴BE=CE,
(2)∵AD是等边△ABC的高,
∴∠CAD=
∠BAC=30°,
∴△AEF为等腰三角形,
∴腰为AE或AF,AE=AF,
∴∠AEF=∠AFE=75°,
∵∠ACB=60°,
∴∠CBF=∠AFE-∠ACB=75°-60°=15°,
∵BE=CE,
∴∠ECD=∠CBF=15°,
故答案为AE或AF
(3)EF=EG,
理由:∵∠BAC=60°,∠FEG=120°,
∴∠BAC+∠FEG=180°,
∴∠AGE+∠AFE=180°,
∴∠AFE=BGE,
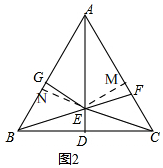
过点E作EN⊥AB,EM⊥AC,
∵AD是∠BAC的平分线,
∴EN=EM;
在△ENG和△EMF中,
,
∴△ENG≌△EMF,
∴EG=EF
 (1)∵AD是等边△ABC的高,
(1)∵AD是等边△ABC的高,∴AD是BC的垂直平分线,
∵点E在AD上,
∴BE=CE,
(2)∵AD是等边△ABC的高,
∴∠CAD=
| 1 |
| 2 |
∴△AEF为等腰三角形,
∴腰为AE或AF,AE=AF,
∴∠AEF=∠AFE=75°,
∵∠ACB=60°,
∴∠CBF=∠AFE-∠ACB=75°-60°=15°,
∵BE=CE,
∴∠ECD=∠CBF=15°,
故答案为AE或AF
(3)EF=EG,
理由:∵∠BAC=60°,∠FEG=120°,
∴∠BAC+∠FEG=180°,
∴∠AGE+∠AFE=180°,
∴∠AFE=BGE,
过点E作EN⊥AB,EM⊥AC,
∵AD是∠BAC的平分线,
∴EN=EM;
在△ENG和△EMF中,
|
∴△ENG≌△EMF,
∴EG=EF
看了 已知AD是等边△ABC的高,...的网友还看了以下:
已知(X为卤原子,M为烃基或含酯基的取代基等).由有机物A合成G(香豆素)的路线如下:请回答下列问 2020-05-02 …
如图,正方形ABCD的边长为1,G是CD边上的一个动点(G不与C、D重合),以CG为一边向正方如图 2020-05-16 …
一种人工合成的信使RNA只含两中核甘酸C和G,其中C的含量是G的2倍,这种人工合成的信使RNA理论 2020-06-04 …
贝诺酯临床主要用于治疗类风湿性关节炎、感冒发烧等.合成路线如下:(1)贝诺酯的分子式.(2)A→B 2020-06-30 …
已知集合A={5,6,7,8},设f,g都是由A到A的映射,其对应法则分别如表1和表2所示:则与f 2020-07-13 …
丙酮是一种常用的有机溶剂,也是合成很多有机化合物的重要原料.由丙酮合成药物G的路线如图:(1)写出化 2020-11-05 …
遗传物质控制蛋白质合成的时候,氨基酸对应的密码子是DNA上的同步还是mRNA?DNA链碱基序列G-C 2020-12-21 …
丙酮是一种常用的有机溶剂,也是合成很多有机化合物的重要原料.由丙酮合成药物G的路线如下:(1)写出化 2020-12-22 …
数据结构论述题,假设在树中,结点x是结点y的双亲时,用(x,y)来表示树边.已知一棵树边的集合为:{ 2020-12-23 …
如图,在正方形ABCD中,G是BC上的任意一点(G与B,C两点不重合),E,F是AG上的两点(E,F 2021-01-11 …