早教吧作业答案频道 -->数学-->
已知抛物线y=ax2+bx+c的顶点为(1,0),与y轴的交点坐标为(0,14).R(1,1)是抛物线对称轴l上的一点.(1)求抛物线y=ax2+bx+c的解析式;(2)若P是抛物线上的一个动点(如图一),求证
题目详情
已知抛物线y=ax2+bx+c的顶点为(1,0),与y轴的交点坐标为(0,
).R(1,1)是抛物线对称轴l上的一点.
(1)求抛物线y=ax2+bx+c的解析式;
(2)若P是抛物线上的一个动点(如图一),求证:点P到R的距离与点P到直线y=-1的距离恒相等;
(3)设直线PR与抛物线的另一交点为Q,E为线段PQ的中点,过点P、E、Q分别作直线y=-1的垂线.垂足分别为M、F、N(如图二).求证:PF⊥QF.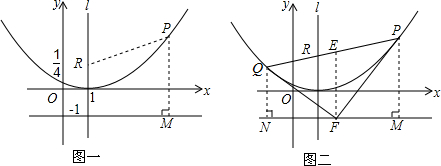
| 1 |
| 4 |
(1)求抛物线y=ax2+bx+c的解析式;
(2)若P是抛物线上的一个动点(如图一),求证:点P到R的距离与点P到直线y=-1的距离恒相等;
(3)设直线PR与抛物线的另一交点为Q,E为线段PQ的中点,过点P、E、Q分别作直线y=-1的垂线.垂足分别为M、F、N(如图二).求证:PF⊥QF.
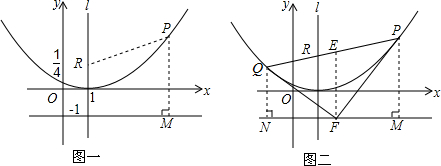
▼优质解答
答案和解析
(1) 设抛物线解析式为y=a(x-1)2,
把(0,
)代入得a=
,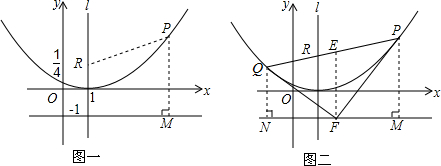
所以抛物线解析式为y=
(x-1)2;
(2)证明:如图1,设P(x,
(x-1)2),则PM=
(x-1)2+1,
∵PR2=(x-1)2+[
(x-1)2-1]2=(x-1)2+[
(x-1)]4-
(x-1)2+1=[
(x-1)]4+
(x-1)2+1=[
(x-1)2+1]2,
∴PR=
(x-1)2+1,
∴PR=PM,
即点P到R的距离与点P到直线y=-1的距离恒相等;
(3)证明:由(2)得QN=QR,PR=PM,
∴PQ=PR+QR=PM+QN,
∵EF⊥MN,QN⊥MN,PM⊥MN,
而E为线段PQ的中点,
∴EF为梯形PMNQ的中位线,
∴EF=
(QN+PM),
∴EF=
PQ,
∴EF=EQ=EP,
∴点F在以PQ为直径的圆上,
∴∠PFQ=90°,
∴PF⊥QF.
把(0,
| 1 |
| 4 |
| 1 |
| 4 |
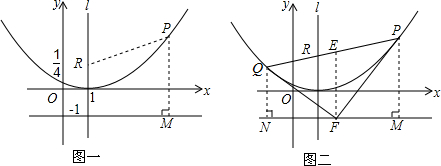
所以抛物线解析式为y=
| 1 |
| 4 |
(2)证明:如图1,设P(x,
| 1 |
| 4 |
| 1 |
| 4 |
∵PR2=(x-1)2+[
| 1 |
| 4 |
| 1 |
| 4 |
| 1 |
| 2 |
| 1 |
| 4 |
| 1 |
| 2 |
| 1 |
| 4 |
∴PR=
| 1 |
| 4 |
∴PR=PM,
即点P到R的距离与点P到直线y=-1的距离恒相等;
(3)证明:由(2)得QN=QR,PR=PM,
∴PQ=PR+QR=PM+QN,
∵EF⊥MN,QN⊥MN,PM⊥MN,
而E为线段PQ的中点,
∴EF为梯形PMNQ的中位线,
∴EF=
| 1 |
| 2 |
∴EF=
| 1 |
| 2 |
∴EF=EQ=EP,
∴点F在以PQ为直径的圆上,
∴∠PFQ=90°,
∴PF⊥QF.
看了 已知抛物线y=ax2+bx+...的网友还看了以下:
已知角MON=45°,其内不有一点P,点P关于OM的对称点为A,关于ON对称点B已知角MON=45 2020-05-02 …
在平面直角坐标系xOy中,C的半径为r,P是与圆心C不重合的点,点P关于C的反称点的定义如下:若在 2020-07-08 …
(2014•聊城)如图,点P是∠AOB外的一点,点M,N分别是∠AOB两边上的点,点P关于OA的对 2020-07-15 …
(2014•鄂州)下面四幅图中,哪一幅图P点位置同时符合下列四个条件()①东半球②北半球③低纬度④ 2020-07-16 …
如图,点P是∠AOB外的一点,点M,N分别是∠AOB两边上的点,点P关于OA的对称点Q恰好落在线段 2020-07-21 …
如图,点P(a,b)和点Q(c,d)是反比例函数y=1x图象上第一象限内的两个动点(a<b,a≠c 2020-07-29 …
已知函数f(x)=﹛2x²+4x+1x<0,﹙1/2﹚xx≥0若图像上有P、Q两点且P、Q关于原点 2020-08-01 …
如果两个图形关于原点O中心对称,其中一个图形上点P的坐标是(-3,5),那么P点在另一个图形上关于 2020-08-03 …
如图,在数轴上,A1,P两点表示的数分别是1,2,A1,A2关于点O对称,A2,A3关于点P对称,A 2020-10-31 …
下图A、B、C、D分别表示几种环境因素对小麦光合作用速率的影响,A、B、C各图,除所示因素外,其他因 2020-12-03 …