早教吧作业答案频道 -->数学-->
已知四棱锥P-ABCD的底面ABCD是菱形,∠ADC=120°,AD的中点M是顶点P的底面ABCD的射影,N是PC的中点.(Ⅰ)求证:平面MPB⊥平面PBC;(Ⅱ)若MP=MC,求直线BN与平面PMC所成角的正弦值.
题目详情
已知四棱锥P-ABCD的底面ABCD是菱形,∠ADC=120°,AD的中点M是顶点P的底面ABCD的射影,N是PC的中点.
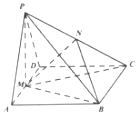
(Ⅰ)求证:平面MPB⊥平面PBC;
(Ⅱ)若MP=MC,求直线BN与平面PMC所成角的正弦值.

(Ⅰ)求证:平面MPB⊥平面PBC;
(Ⅱ)若MP=MC,求直线BN与平面PMC所成角的正弦值.
▼优质解答
答案和解析
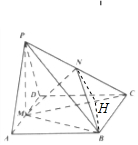 (Ⅰ)证明:在菱形ABCD中,设AB=2a,M是AD的中点,
(Ⅰ)证明:在菱形ABCD中,设AB=2a,M是AD的中点,
MB2=AM2+AB2-2AM•AB•cos60°=3a2,MC2=DM2+DC2-2DM•DC•cos120°=7a2.
又∵BC2=4a2,∴MB2+BC2=MC2,∴MB⊥BC,
又∵P在底面ABCD的射影M是AD的中点,∴PM⊥平面ABCD,
又∵BC⊂平面ABCD,∴PM⊥BC,
而PM∩MB=M,PM,MB⊂平面PMB,∴BC⊥平面PMB,
又BC⊂平面PBC,∴平面MPB⊥平面PBC.
(Ⅱ) 过B作BH⊥MC,连接HN,
∵PM⊥平面ABCD,BC⊂平面ABCD,∴BH⊥PM,
又∵PM,MC⊂平面PMC,PM∩MC=M,∴BH⊥平面PMC,
∴HN为直线BN在平面PMC上的射影,
故∠BNH为直线BN与平面PMC所成的角,
在△MBC中,BH=
=
a
由(Ⅰ)知BC⊥平面PMB,PB⊂平面PMB,∴PB⊥BC.
BN=
PC=
a,
∴sin∠BNH=
=
=
.
 (Ⅰ)证明:在菱形ABCD中,设AB=2a,M是AD的中点,
(Ⅰ)证明:在菱形ABCD中,设AB=2a,M是AD的中点,MB2=AM2+AB2-2AM•AB•cos60°=3a2,MC2=DM2+DC2-2DM•DC•cos120°=7a2.
又∵BC2=4a2,∴MB2+BC2=MC2,∴MB⊥BC,
又∵P在底面ABCD的射影M是AD的中点,∴PM⊥平面ABCD,
又∵BC⊂平面ABCD,∴PM⊥BC,
而PM∩MB=M,PM,MB⊂平面PMB,∴BC⊥平面PMB,
又BC⊂平面PBC,∴平面MPB⊥平面PBC.
(Ⅱ) 过B作BH⊥MC,连接HN,
∵PM⊥平面ABCD,BC⊂平面ABCD,∴BH⊥PM,
又∵PM,MC⊂平面PMC,PM∩MC=M,∴BH⊥平面PMC,
∴HN为直线BN在平面PMC上的射影,
故∠BNH为直线BN与平面PMC所成的角,
在△MBC中,BH=
2a•
| ||
|
2
| ||
| 7 |
由(Ⅰ)知BC⊥平面PMB,PB⊂平面PMB,∴PB⊥BC.
BN=
| 1 |
| 2 |
| ||
| 2 |
∴sin∠BNH=
| BH |
| BN |
| ||||
|
2
| ||
| 7 |
看了 已知四棱锥P-ABCD的底面...的网友还看了以下:
1、该沙尘暴发生地位于[B]A.副极地低压带B.西风带C.副热带高压带D.东北信风带2、影像中部显示 2020-03-30 …
读“经纬网图”,完成下列要求.(1)写出图中A、B、C、D四点的经纬度:A.;B.;C.;D..( 2020-05-02 …
关于开普勒三定律下列论述正确的是:A.在公式中,a是行星中心到太阳中心的距离B.在公式中,k是行星 2020-05-13 …
一中子与一质量数为A(A>1)的原子核发生弹性正碰.若碰前原子核静止,则碰撞前与碰撞后中子的速率之 2020-05-13 …
关于下列铁路枢纽交会正确的是()A.郑州站中A为京广线,B为陇海线B.兰州站中A为沪杭线,B为兰新 2020-06-21 …
1.对于双链DNA而言,若一条链中(A+G)/(T+C)=0.7,则:(1)互补链中(A+G)/( 2020-06-26 …
已知A是一个3×4矩阵,下列命题中正确的是()A.若矩阵A中所有3阶子式都为0,则秩(A)=2B. 2020-06-30 …
读下图,回答19~20题。19.图中a、b、c三种铁路选线方案中,合理的是A.aB.bC.cD.a 2020-07-16 …
化简的题1.B∠A∠0∠1∠C("∠"为小于符号)|A|=|B|化简|A|÷A+|B|÷B+|C| 2020-08-01 …
下列推理正确的是()A.如果不买彩票,那么就不能中奖.因为你买了彩票,所以你一定中奖B.因为a>b, 2020-12-03 …