早教吧作业答案频道 -->数学-->
如图,PB为⊙O的切线,B为切点,过B作OP的垂线BA,垂足为C,交⊙O于点A,连接PA,AO,并延长AO交⊙O于点E,与PB的延长线交于点D.(1)求证:PA是⊙O的切线;(2)若cos∠CAO=45,且OC=6,求PB
题目详情
如图,PB为⊙O的切线,B为切点,过B作OP的垂线BA,垂足为C,交⊙O于点A,连接PA,AO,并延长AO交⊙O于点E,与PB的延长线交于点D.
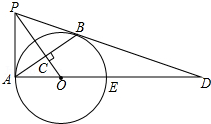
(1)求证:PA是⊙O的切线;
(2)若cos∠CAO=
,且OC=6,求PB的长.

(1)求证:PA是⊙O的切线;
(2)若cos∠CAO=
| 4 |
| 5 |
▼优质解答
答案和解析
(1)连接OB.
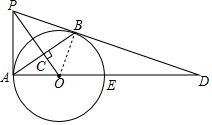
∵OA=OB,
∴∠OAB=∠OBA.
∵OP⊥AB,
∴AC=BC.
∴OP是AB的垂直平分线,
∴PA=PB.
∴∠PAB=∠PBA.
∴∠PAO=∠PBO.
∵PD为⊙O的切线,
∴∠OBP=90°.
∴∠PAO=90°.
∴PA是⊙O的切线.
(2)设AC=4k,AO=5k,由勾股定理可知OC=3k,
∴sin∠CAO=
,tan∠COA=
∴
=
,即
=
,解得OA=10.
∵tan∠POA=
=
,
∴
=
,解得AP=
.
∵PA和PB均为⊙的切线,
∴PB=PA=
.

∵OA=OB,
∴∠OAB=∠OBA.
∵OP⊥AB,
∴AC=BC.
∴OP是AB的垂直平分线,
∴PA=PB.
∴∠PAB=∠PBA.
∴∠PAO=∠PBO.
∵PD为⊙O的切线,
∴∠OBP=90°.
∴∠PAO=90°.
∴PA是⊙O的切线.
(2)设AC=4k,AO=5k,由勾股定理可知OC=3k,
∴sin∠CAO=
| 3 |
| 5 |
| 4 |
| 3 |
∴
| CO |
| OA |
| 3 |
| 5 |
| 6 |
| OA |
| 3 |
| 5 |
∵tan∠POA=
| AP |
| AO |
| 4 |
| 3 |
∴
| AP |
| 10 |
| 4 |
| 3 |
| 40 |
| 3 |
∵PA和PB均为⊙的切线,
∴PB=PA=
| 40 |
| 3 |
看了 如图,PB为⊙O的切线,B为...的网友还看了以下:
读“大陆空气柱图”,图中圆柱为空气柱,箭头表示空气垂直运动方向.据此完成35-36题.35.关于a 2020-05-02 …
该图是某群岛白昼长短月变化示意图,读图回答3~4题。小题1:该群岛大致位于A.66°34′NB.7 2020-05-13 …
(2012•云南)如图,在平面直角坐标系中,直线y=−13x+2交x轴于点P,交y轴于点A.抛物线 2020-06-29 …
该图是某群岛白昼长短月变化示意图,读图回答下题。小题1:该群岛大致位于A.66°34′NB.70° 2020-06-30 …
3.某设备于1990年12月购进,账面价值为200万元,购进时的定基物价指数为102%,2008年 2020-07-18 …
对于线性相关系数,叙述正确的是()A.|r|≤1,|r|越接近于1,相关程度越弱,|r|越接近于0 2020-08-02 …
政治权力由“传贤”演化为“传子”,“家天下”制度开始形成于()A.黄帝时代B.夏朝政治权力由“传贤” 2020-11-04 …
两灯塔A,B与海洋观察站C的距离都等于a(km),灯塔A在C北偏东30°,B在C南偏东60°,则A, 2020-11-13 …
相向运动的A.B两辆小车相撞后,一同沿A原来的方向前进,则碰撞前的瞬间()A.A车的速度一定大于B车 2020-11-30 …
氢原子从n=2的激发态跃迁到基态时辐射的光子为a,从n=3的激发态跃迁到基态时辐射的光子为b,下列说 2020-12-30 …