早教吧作业答案频道 -->数学-->
如图,直线l1:y=2x+3与y轴交于点B,直线l2交y轴于点A(0,-1),且直线l1与直线l2交于点P(-1,t).(1)求直线l2的函数表达式;(2)过动点D(a,0)作x轴的垂线与直线l1,l2分别交于M,N两
题目详情
如图,直线l1:y=2x+3与y轴交于点B,直线l2交y轴于点A(0,-1),且直线l1与直线l2交于点P(-1,t).
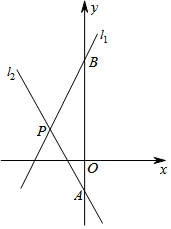
(1)求直线l2的函数表达式;
(2)过动点D(a,0)作x轴的垂线与直线l1,l2分别交于M,N两点,且MN≤2.
①求a的取值范围;
②若S△APM=
S△AMB,求MN的长度.

(1)求直线l2的函数表达式;
(2)过动点D(a,0)作x轴的垂线与直线l1,l2分别交于M,N两点,且MN≤2.
①求a的取值范围;
②若S△APM=
| 1 |
| 2 |
▼优质解答
答案和解析
(1)∵点P(-1,t)在直线直线l1上,
∴t=2×(-1)+3=1,即P(-1,1),
设直线l2解析式为y=kx+b,
把A、P的坐标代入可得
,解得
,
∴直线l2的函数表达式为y=-x-1;
(2)①∵MN∥y轴,
∴M、N的横坐标为a,
设M、N的纵坐标分别为ym和yn,
∴ym=2a+3,yn=-a-1,
当MN在点P左侧时,此时a<-1,
则有MN=yn-ym=-a-1-(2a+3)=-3a-4,
∵MN≤2,
∴-3a-4≤2,解得a≥-2,
∴此时-2≤a<-1;
当MN在点P的右侧时,此时a>-1,
则有MN=ym-yn=2a+3-(-a-1)=3a+4,
∵MN≤2,
∴3a+4≤2,解得a≤-
,
∴此时-1<a<-
;
综上可知当-2≤a<-1或-1<a<-
时,MN≤2;
②由题意可知B(0,3),且A(0,-1),
∴AB=4,
∵P(-1,1),
∴S△APB=
×4×1=2,
由题意可知点M只能在y轴的右侧,
当点M在线段AP上时,过点M作MC⊥y轴于点C,如图1
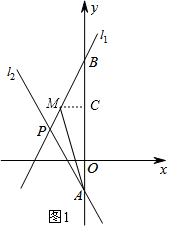
∵S△APM=
S△AMB,
∴S△ABM=
S△APB=
,
∴
AB•MC=
,即2MC=
,解得MC=
,
∴点M的横坐标为-
,即a=-
,
∴MN=3a+4=-2+4=2;
当点M在线段BP的延长线上时,过点M作MD⊥y轴于点D,如图2,
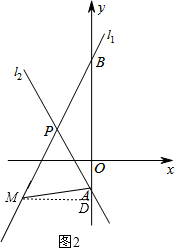
∵S△APM=
S△AMB,
∴S△ABM=2S△APB=4,
∴
AB•MC=4,即2MC=4,解得MC=2,
∴点M的横坐标为-2,
∴MN=-3a-4=6-4=2,
综上可知MN的长度为2.
(1)∵点P(-1,t)在直线直线l1上,
∴t=2×(-1)+3=1,即P(-1,1),
设直线l2解析式为y=kx+b,
把A、P的坐标代入可得
|
|
∴直线l2的函数表达式为y=-x-1;
(2)①∵MN∥y轴,
∴M、N的横坐标为a,
设M、N的纵坐标分别为ym和yn,
∴ym=2a+3,yn=-a-1,
当MN在点P左侧时,此时a<-1,
则有MN=yn-ym=-a-1-(2a+3)=-3a-4,
∵MN≤2,
∴-3a-4≤2,解得a≥-2,
∴此时-2≤a<-1;
当MN在点P的右侧时,此时a>-1,
则有MN=ym-yn=2a+3-(-a-1)=3a+4,
∵MN≤2,
∴3a+4≤2,解得a≤-
| 2 |
| 3 |
∴此时-1<a<-
| 2 |
| 3 |
综上可知当-2≤a<-1或-1<a<-
| 2 |
| 3 |
②由题意可知B(0,3),且A(0,-1),
∴AB=4,
∵P(-1,1),
∴S△APB=
| 1 |
| 2 |
由题意可知点M只能在y轴的右侧,
当点M在线段AP上时,过点M作MC⊥y轴于点C,如图1

∵S△APM=
| 1 |
| 2 |
∴S△ABM=
| 2 |
| 3 |
| 4 |
| 3 |
∴
| 1 |
| 2 |
| 4 |
| 3 |
| 4 |
| 3 |
| 2 |
| 3 |
∴点M的横坐标为-
| 2 |
| 3 |
| 2 |
| 3 |
∴MN=3a+4=-2+4=2;
当点M在线段BP的延长线上时,过点M作MD⊥y轴于点D,如图2,

∵S△APM=
| 1 |
| 2 |
∴S△ABM=2S△APB=4,
∴
| 1 |
| 2 |
∴点M的横坐标为-2,
∴MN=-3a-4=6-4=2,
综上可知MN的长度为2.
看了 如图,直线l1:y=2x+3...的网友还看了以下:
抛物线y=2x^2上的点到直线4x-3y+1=0的距离最小值为?答案是求抛物线导函数,然后求出当抛物 2020-03-30 …
(2014•内江模拟)已知直线l与直线x+y=1=0垂直,其纵截距b=-3,椭圆C的两个焦点为F1 2020-06-12 …
在平面直角坐标系xOy中,点P在由直线,直线和直线所围成的区域内或其边界上,点Q在x轴上,若点R的 2020-06-14 …
如图1所示,长方体金属块在细绳竖直向上拉力作用下从水中开始一直竖直向上做匀速直线运动,直至长方体下 2020-06-27 …
已知正比例函数y=3x图象上点P的横坐标为-2,点P关于x轴,y轴的对称点分别为P1和P2.(1) 2020-07-22 …
利用直尺画图(1)利用图1中的网格,过P点画直线AB的平行线和垂线.(2)把图(2)网格中的三条线 2020-07-29 …
物体运动的位移随时间的变化而变化,这种变化规律可以用数学图象表示出来,在平面直图象角坐标系中,用纵 2020-07-30 …
如图1,将两根笔直细木板MN、EF用图钉固定并平行摆放,将一根橡皮筋拉直后用图钉分别固定在MN、E 2020-07-30 …
一列横波沿一条直线向右传播,O、B为直线上相距不远的两点,O为波源,从O点开始振动起经0.3s传到B 2020-12-18 …
抛物线与直线直线与抛物线相切,切线长为根号十五.抛物线方程为:Y的平方等于负四X.直线斜率为二,求直 2021-01-04 …