早教吧作业答案频道 -->数学-->
在Rt△ABC中,BC=AC,∠ACB=90°,点D为射线AB上一点,连接CD,过点C作线段CD的垂线l,在直线l上,分别在点C的两侧截取与线段CD相等的线段CE和CF,连接AE、BF.(1)当点D在线段AB上时(点D不
题目详情
在Rt△ABC中,BC=AC,∠ACB=90°,点D为射线AB上一点,连接CD,过点C作线段CD的垂线l,在直线l上,分别在点C的两侧截取与线段CD相等的线段CE和CF,连接AE、BF.
(1)当点D在线段AB上时(点D不与点A、B重合),如图1
①请你将图形补充完整;
②线段BF、AD所在直线的位置关系为___,线段BF、AD的数量关系为___;
(2)当点D在线段AB的延长线上时,如图2
①请你将图形补充完整;
②在(1)中②问的结论是否仍然成立?如果成立请进行证明,如果不成立,请说明理由.
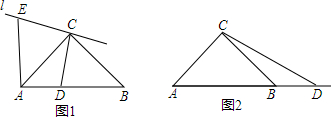
(1)当点D在线段AB上时(点D不与点A、B重合),如图1
①请你将图形补充完整;
②线段BF、AD所在直线的位置关系为___,线段BF、AD的数量关系为___;
(2)当点D在线段AB的延长线上时,如图2
①请你将图形补充完整;
②在(1)中②问的结论是否仍然成立?如果成立请进行证明,如果不成立,请说明理由.

▼优质解答
答案和解析
(1)①见图1所示.
②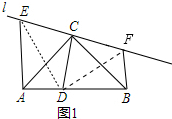 证明:连接ED,DF.
证明:连接ED,DF.
∵CD⊥EF,
∴∠DCF=90°,
∵∠ACB=90°,
∴∠ACB=∠DCF,
∴∠ACD=∠BCF
∵BC=AC,CD=CF,
∴△ACD≌△BCF,
∴AD=BF,∠BAC=∠FBC,
∴∠ABF=∠ABC+∠FBC=∠ABC+∠BAC=90°,
即BF⊥AD.
故答案为:垂直、相等.
(2)①见图2所示.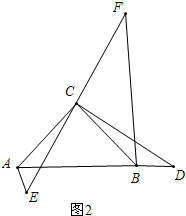
②成立.理由如下:
证明:∵CD⊥EF,
∴∠DCF=90°,
∵∠ACB=90°,
∴∠DCF+∠BCD=∠ACB+∠BCD,
即∠ACD=∠BCF,
∵BC=AC,CD=CF,
∴△ACD≌△BCF,
∴AD=BF,∠BAC=∠FBC,
∴∠ABF=∠ABC+∠FBC=∠ABC+∠BAC=90°,
即BF⊥AD.
②
 证明:连接ED,DF.
证明:连接ED,DF.∵CD⊥EF,
∴∠DCF=90°,
∵∠ACB=90°,
∴∠ACB=∠DCF,
∴∠ACD=∠BCF
∵BC=AC,CD=CF,
∴△ACD≌△BCF,
∴AD=BF,∠BAC=∠FBC,
∴∠ABF=∠ABC+∠FBC=∠ABC+∠BAC=90°,
即BF⊥AD.
故答案为:垂直、相等.
(2)①见图2所示.

②成立.理由如下:
证明:∵CD⊥EF,
∴∠DCF=90°,
∵∠ACB=90°,
∴∠DCF+∠BCD=∠ACB+∠BCD,
即∠ACD=∠BCF,
∵BC=AC,CD=CF,
∴△ACD≌△BCF,
∴AD=BF,∠BAC=∠FBC,
∴∠ABF=∠ABC+∠FBC=∠ABC+∠BAC=90°,
即BF⊥AD.
看了 在Rt△ABC中,BC=AC...的网友还看了以下:
设AB是圆O的一定弦,C是AB上一个固定点,过C任意作弦XY,设MN分别是AB及XY的中点.证明: 2020-04-07 …
ACB等腰直角三角型C为直角AC等于BC,D为BC中点,过C点作垂直线交AD于F点,交AB于E点, 2020-05-17 …
如图,AB为圆O的直径,C为圆上任意一点,过C的切线分别与过点A,B两点的切线交于P,Q,求证AB 2020-06-04 …
如图c为圆o直径上一点.过c点作玄de.使cd=co,若狐ad的度数为50°.求狐be的度数 2020-07-02 …
P是圆外一点,PA,PB分别和⊙O相切于A,B,PA=PB=4CMP是圆外一点,PA,PB分别和圆 2020-07-20 …
如图,平行于x轴的直线AC分别交抛物线y1=x的平方于y=三分之一x的平方与BC两点,过C作y轴如 2020-07-29 …
已知直线y=1/2x+3分别交x轴y轴于点AB点C是该直线与反比例函数y=k/x的图像在第一象限内 2020-08-01 …
(2013•潍坊二模)如图所示,14圆形玻璃砖放在水平桌面上,圆心为O,半径为R,激光束垂直OB射向 2020-11-13 …
在直角三角形ABC中,角C等于90度,AC=BC,点D是AB边上的中点,过c引一条直线l(不与acb 2020-11-28 …
(2014•衡阳三模)如图为半圆形的玻璃砖,C为AB的中点,OO′为过点C的AB面的垂线,a、b两束 2020-12-18 …