早教吧作业答案频道 -->数学-->
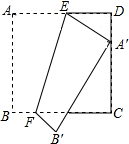
如图,正方形纸片ABCD的边长为12,E,F分别是边AD,BC上的点,将正方形纸片沿EF折叠,使得点A落在CD边上的点A′处,此时点落在点B′处.已知折痕EF=13,则AE的长等于.
题目详情
如图,正方形纸片ABCD的边长为12,E,F分别是边AD,BC上的点,将正方形纸片沿EF折叠,使得点A落在CD边上的点A′处,此时点落在点B′处.已知折痕EF=13,则AE的长等于___.

▼优质解答
答案和解析
过点F作FG⊥AD,垂足为G,连接AA′.
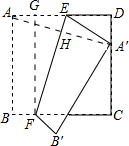
在Rt△EFG中,EG=
=
=5.
∵轴对称的性质可知AA′⊥EF,
∴∠EAH+∠AEH=90°.
∵FG⊥AD,
∴∠GEF+∠EFG=90°.
∴∠DAA′=∠GFE.
在△GEF和△DA′A中,
,
∴△GEF≌△DA′A.
∴DA′=EG=5.
设AE=x,由翻折的性质可知EA′=x,则DE=12-x.
在Rt△EDA′中,由勾股定理得:EA′2=DE2+A′D2,即x2=(12-x)2+52.
解得:x=
.
故答案为:
.

在Rt△EFG中,EG=
| EF2-FG2 |
| 132-122 |
∵轴对称的性质可知AA′⊥EF,
∴∠EAH+∠AEH=90°.
∵FG⊥AD,
∴∠GEF+∠EFG=90°.
∴∠DAA′=∠GFE.
在△GEF和△DA′A中,
|
∴△GEF≌△DA′A.
∴DA′=EG=5.
设AE=x,由翻折的性质可知EA′=x,则DE=12-x.
在Rt△EDA′中,由勾股定理得:EA′2=DE2+A′D2,即x2=(12-x)2+52.
解得:x=
| 169 |
| 24 |
故答案为:
| 169 |
| 24 |
看了 如图,正方形纸片ABCD的边...的网友还看了以下:
(8分)如图,为了解某海域海底构造,在海平面内一条直线上的A,B,C三点进行测量,已知,,于A处测 2020-05-16 …
以下关于(C)处的说法,正确的是( )。 A.(C)处应填人“适用于上市公司”B.(C)处所对应的 2020-05-30 …
A,B,C三重量的关系式是A乘B等于C(A,B,C均不等于0)A,B,C三重量的关系式是A乘B等于 2020-06-03 …
图5中abcd四点间存在热力环流,根据四点气压数值判断下列说法正确的是A.由于a处气压低于c处,所 2020-06-12 …
如图是血液流经某一组织的示意图,下列相关说法,正确的是()A.若A是胰岛细胞,饭后一小时,b处胰岛 2020-07-03 …
如图所示,在倾角为37°的斜面上,一劲度系数为k=100N/m的轻弹簧一端固定在A点,自然状态时另 2020-07-31 …
如图,为了解某海域海底构造,在海平面内一条直线上的A,B,C三点进行测量,已知AB=50m,BC= 2020-08-02 …
若a大于b大于c,且a+c+b=0,则下列不等式中正确的是A,ab大于acB,a若a大于b大于c, 2020-08-03 …
图地球公转示意图(地球位于两分两至位置),回答下列问题.(1)地球位于A处时,日期是前后,北半球的节 2020-11-06 …
(2014•常州一模)如图是小明同学制作的针孔照相机,分别调整内、外纸筒和蜡烛的位置,保证都能在半透 2020-11-12 …